インダクタンスとは何か？計算方法・公式、例題で解説！

インダクタンスというコイルの性質をご存知でしょうか。インダクタンスとはコイルにおいて電流の変化が誘導起電力となって現れる性質です。しばしば、誘導係数、誘導子とも呼ばれます。インダクタンスの性質は第三種電気主任技術者試験にも出題されることがある重要な理論です。この記事では、そんなインダクタンスについて、自己インダクタンスと相互インダクタンスそれぞれを紹介しながら数式・公式・計算を用いて解説していきます。

▼すでに電験資格をお持ちの方
電験保有者は引く手数多。『電気主任技術者の転職エピソード』や『未経験からの転職事情』などもご覧ください

1 インダクタンスとは？数式や公式で読み解く、電流との関係、単位
2 [インダクタンス]自己インダクタンスの公式・計算
3 [インダクタンス]相互インダクタンスとは？計算・公式
4 インダクタンスを求める計算の例題
5 まとめ

インダクタンスとは？数式や公式で読み解く、電流との関係、単位

インダクタンスの性質は電流の変化で生じる、インダクタンスの単位とは？

インダクタンスとは、コイルなどにおいて電流の変化が誘導起電力となって現れる性質です。導体に電流を流した場合には、電圧降下が生じます。しかし、電流が時間的に変化する場合には、わずかではあるが変化の割合に応じて抵抗とは別の電圧降下が生じます。導体がコイル状になっている場合には、この電圧降下はかなり大きくなり、無視できなくなります。この現象のことを電磁誘導現象と呼びます。

図1相互結合された二つのコイル

図1に示すコイルに電流 $i(t)$ を流した時に生じる磁束を $\Phi(t)[Wb]$ とすると、ファラデーの電磁誘導法則によって $N$ 回巻きのコイルの両側に生じる電圧 $v(t)$ は、

$v(t)=N\frac{d\Phi(t)}{dt}=\frac{d}{\phi(t)}$

[右辺 $\phi(t)$ を全磁束]

となり、コイルが空心の場合には、 $i(t)$ と $\phi$ は比例するので、以下のように表すことができます。

$\phi(t)=Li(t)$

この比例定数 $L$ のことを自己インダクタンスと呼びます。自己インダクタンスの単位はヘンリーで、[H]を用います。空心の場合には、 $i(t)$ と $v(t)$ の関係は、以下のようになります。

$v(t)=\frac{d\phi}{dt}=L\frac{di}{dt}$

電流が変化することによって、コイルの両端に電圧降下が生じることになり、言い換えると以下のように表すことができるのです。

$i(t)=\frac{1}{L}\int_{-\infty}^{t}v(\tau)d\tau$

$=\frac{1}{L}\int_{-\infty}^{0}v(\tau)d\tau+\frac{1}{L}\int_{0}{t}v(\tau)d\tau$

$=i_0+\frac{1}{L}\int_{0}^{t}v(\tau)d(\tau)$

となります。もしくは、

$\phi(t)=\phi_0+\int_{0}^{t}v(\tau)d\tau$

となります。ここで、 $i_0$ および $\phi_0$ は、それぞれ $t=0$ において、インダクタンスに流れた電流及びインダクタンスに生じていた全磁束です。上の二つの式からわかるように、初期電流 $i_0$ をゼロとする代わりに、インダクタンスに並列に電流源 $i_0$ を接続してもよいのです。

次に、 $t$ →0でとした場合について考慮すると、 $v(t)$ が $t=0$ で無限大のジャンプをしない限り、

$\lim_{t \to 0}\int_{0}^{t}v(\tau)d\tau=0$

であることがわかります。したがって、インダクタンスに流れる電流、もしくは磁束(全磁束)は $v(t)$ が無限大のジャンプをしない限り任意の瞬間において連続的であるということができます。インダクタンスは巻き数が多く輪が大きいほど大きな値になり、鉄心を挿入してコイルの性質を強めたりすることができ、コイルの電流は他のコイルにも影響を与えているのです。これがインダクタンスの性質です。

[インダクタンス]自己インダクタンスの公式・計算

先ほどのインダクタンスの性質で少し触れた自己インダクタンスにもう少し踏み込んで解説していきます。

自己インダクタンスとは？数式・公式・計算

コイルに流れる電流が変化すると、電流の変化が磁束の変化となり、コイルに起電力を誘起します。この作用のことを自己誘導作用といいます。この起電力を自己誘導起電力と呼びます。自己誘導作用による自己誘導起電力 $e$ は、電流の変化の割合(電流の変化率) $\Delta I/\Delta t$ に比例します。

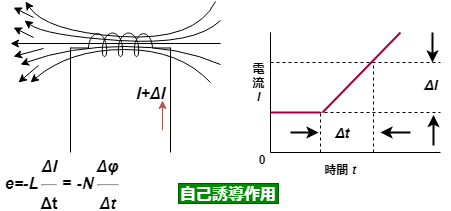
先ほども触れたようにここでの比例定数は $L$ で、 $L$ はコイルの性質を表している定数で、これを自己インダクタンス(単位はヘンリー[H])と呼ぶのでした。自己インダクタンスは、電流の変化によってコイル自身に生じる起電力の大きさの量というわけです。

$e=-L\frac{\Delta I}{\Delta t}[V]....(1)$

起電力の式に負の符号がついていますが、これは、電流の変化を妨げる方向に起電力が発生することを指しています。このことを逆起電力といいます。また、巻線を貫く磁束が変化すると、磁束の変化を打ち消す方っ港に誘導起電力が発生します。巻き数 $N$ のコイルでは、誘導起電力は以下のようにあらわすことができます。

$e=-N\frac{\Delta \Phi}{\Delta t}[V]....(2)$

ここで、式(1)と(2)は等しいので、

$L\frac{\Delta I}{\Delta t}=N\frac{\Delta \Phi}{\Delta t}$

よって、

$L=N\frac{\Delta \Phi}{\Delta I}[H]$

ここで、コイルの磁束と電流は比例するので、次の式が成立します。

$L=\frac{N\Phi}{I}[H]....(3)$

コイルの巻き数 $N$ と磁束 $\Phi$ の積＝磁束数は、 $(N\Phi)$ となり、このことを磁束鎖交数といいます。つまり、インダクタンス $L$ は、コイルに1Aの電流を流した時の磁束鎖交数となるのです。式(3)より、

$N\Phi=LI$

であるのです。コイルの磁束鎖交数 $(N\Phi)$ は電流 $I$ に比例し、比例定数が自己インダクタンス $L$ となるのです。

環状コイル(ソレノイド)の自己インダクタンス

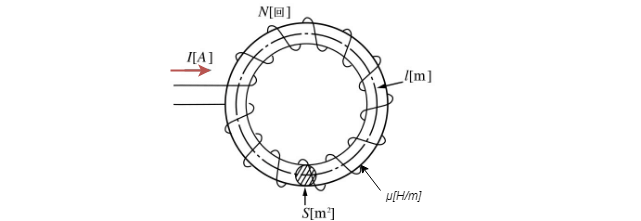
上の図のような環状コイルがあるとします。上図の環状コイルは、 $N$ 回巻の環状コイルで、環状コイルに電流 $I[A]$ を流したときに、鉄心内の磁束を $\Phi[Wb]$ 、磁束密度を $B[T]$ 、鉄心の断面積を $S[m^2]$ として、環状コイルの自己インダクタンス $L[H]$ を求めます。

$L=\frac{N\Phi}{I}=\frac{NSB}{I}=\frac{NS\mu H}{I}$

$=\frac{NS\mu}{I}\frac{NI}{l}$

$=\frac{\mu SN^2}{l}=\frac{N^2}{R_m}[H]$

となります。自己インダクタンス $L$ は、コイルの巻き数 $N$ の二乗に比例することがわかります。一方、磁気抵抗 $R_m$ には反比例していることがわかります。

[インダクタンス]相互インダクタンスとは？計算・公式

相互インダクタンスの性質・計算・公式

独立したコイル $L_1$ に流れる電流 $i_1$ と、その両端の電圧 $v_i$ との関係は以下のように示されるのでした。

$v_1=L_1\frac{di_1}{dt}$

ここで、もう一つのコイル $L_2$ が $L_1$ に近接しておかれてあり、互いに影響を及ぼしあう場合、 $L_2$ に流れる電流 $i_2$ が電磁誘導によって $v_1$ に影響を与えることになります。このとき、 $v_1$ は、

$v_1=L_1\frac{di_1}{dt}+M_{21}\frac{di_2}{dt}$

という形になります。また、 $L_2$ の両端の電圧 $v_2$ も $i_1$ の影響を受け、

$v_2=L_2\frac{di_1}{dt}+M_{12}\frac{di_1}{dt}$

となります。このときの、 $M_{21}$ と $M_{12}$ は値が等しくなるので、 $M_{21}=M_{12}=M$ となり、このことを相互インダクタンスといいます。相互インダクタンスは、コイルの巻き方や電流の向きによって正あるいは負の値をとります。この相互インダクタンスの符号 $M$ はコイルの巻き方、電流の向きによって、 $M>0$ 、 $M<0$ となるということです。

相互インダクタンスの性質を整理すると、二つのコイルがあるとき、一方のコイルに流れる電流が変化すると、もう一方のコイルに起電力が誘導されます。この作用のことを相互誘導作用といい、二つのコイルの間に相互誘導作用があるとき、両コイルは電磁結合しているということができます。つまり、相互誘導作用による誘導起電力は、他方のコイルの電流変化の割合に比例しているのです。相互インダクタンスは、比例定数 $M$ で表せれます。相互インダクタンスの単位は自己インダクタンスと同様にヘンリー[H]です。

相互インダクタンス $M$ は、一つのコイルに1Aを流したときの $L_2$ の磁束鎖交数、もう一つのコイルに1Aを流したときの $L_1$ の磁束鎖交流のそれぞれは次のように表すことができます。

$M=\frac{L_2 \Phi_1}{i_1}[H]$

$M~\frac{L_1 \Phi_2}{i_2}[H]$

相互インダクタンスを含む回路での相互インダクタンスは等価回路になる？

図4相互インダクタンスを含む回路

例として、☝のような回路があるとすると、回路方程式は、以下のようになります。

$R_ii_i+L_1\frac{di_1}{dt}+M\frac{di_2}{dt}=e(t)$

$R_2i_2+L_2\frac{di_2}{dt}+M\frac{di_1}{dt}=0$

ここで、 $e(t)$ が正弦波であり、定常状態を想定し、フェーザ法によってこれを表すと、

$(R+j\omega L_1)\dot{I_1}+j\omega M\dot{I_2}=E$

$j\omega M\dot{I_1}+(R_2+j\omega L_2)\dot{I_2}=0$

これより、 $\dot{I_2}$ を求めると、

$\dot{I_2}=\frac{-j\omega ME}{(R_1+j\omega L_1)(R_2+j\omega L_2)+\omega^2 M^2}$

$=\frac{-j\omega ME}{(R_1 R_2 -\omega^2 L_1 L_2 +\omega^2 M^2)+j\omega(L_1 R_2 +L_2 R_1)}$

$|(\dot{I_2})|=\frac{\omega ME}{\sqrt{{R_1 R_2-\omega(L_1 L_2 -M^2)}^2+\omega^2(L_1 R_2 +L_2 R_1)^2}}$

$\verb|位相差|\phi=tan^-1\frac{-R_1 R_2+\omega^2(L_1 L_2-M^2)}{\omega(L_1 R_2+L_2 R_1)}$

となります。ここで、回路方程式についてを考慮すると、以下のような式になります。

$(R_1+j\omega L_1)\dot{I_1}+l\omega M\dot{I_2}=E$

$j\omega M\dot{I_1}+(R_2+j\omega L_2)\dot{I_2}=0$

図5相互インダクタンスを含む回路:等価回路

といった形になります。この回路方程式は、図5の示す回路方程式になっていることがわかります。すなわち、図4と図5の回路は全く同じ回路方程式が成り立っていることがわかります。したがって、図4の回路の代わりに図5の回路でもよいということになります。相互インダクタンスの回路ではこのような性質があり、両回路の関係は等価回路となります。

インダクタンスを求める計算の例題

自己インダクタンスの値を求める例題

巻数 $N=10$ のコイルのを流れる電流が0.1秒間に0.6Aの割合で変化しているとき、コイルを貫く磁束が0.4秒間に1.2mWbの割合で変化した。子のコイルの自己インダクタンス $L[mH]$ の値として正しいのはどれか？＊ただし、コイルの漏れ磁束は無視できるものとする。

(1)0.5 (2)2.5 (3)5 (4)10 (5)20

解答

①起電力を求める公式より、電流の変化率を求める式=磁束の変化率から求める式なので、

$L\frac{\Delta I}{\Delta t_1}=N\frac{\Delta \Phi}{\Delta t_2}....(1)$

② $N=10$ 、 $\Delta t_1=0.1s$ に変化する電流は $\Delta I=0.6A$ となります。ここで、 $\Delta t_2=0.4s$ に変化する磁束は $\Delta \Phi=1.2\times 10^{-3}Wb$ となります。ゆえに(1)式にこれらの値を代入すると、以下のように求めることができます。