重ね合わせの理とは？電圧・電流源混在の場合等、例題と併せて解説

電源が2個以上の複数ある回路を単純化して解析するときに重ね合わせの理は非常に便利です。電験三種の理論の問題でも重ね合わせの定理は使用することが多い定理の一つです。

この記事ではそんな重ね合わせの理についてを例題、問題を含めて紹介します。

1 重ね合わせの理とは？どんな定理？
2 重ね合わせの理の例題で学ぶ。電流を求める
3 重ね合わせの理を使用し、電圧を解析する
4 電流源と電圧源が混在している複雑な回路の重ね合わせの理
5 交流回路における重ね合わせの理
6 まとめ

重ね合わせの理とは？どんな定理？

電源を取り出し分離電路を重ね合わせる理

重ね合わせの定理は重ねの理とも呼ばれます。重ね合わせの理とは、「2個以上の複数の電源がある回路で、回路の任意の点の電流及び電圧はそれぞれの電源が単独で存在した場合の値の和に等しい」と説明される理論です。

重ね合わせの理は、一つの電源だけを残して他の電源を取り除いた分離回路の電流や電圧を解析することを複数ある電源の数の分だけ取り出すことを繰り返し、得られた電流や電圧を合成していけば、元の回路の電流や電源を求めることができる便利な定理なのです。このような電源ごとの分離回路が重なって見えることから重ね合わせの理(重ねて合わせる)と呼ばれているようです。

重ね合わせの定理はこんな時に使う！電流源を取り除く際は開放

2個以上の複数の電源があるときは電源を一つにして求める理論として、似たものにキルヒホッフの法則があります。
キルヒホッフの法則については「キルヒホッフの法則とは？公式や例題と合わせて解説！」という記事で紹介しています。

キルヒホッフの法則とは、接続点に入る電流と出る電流は同じというキルヒホッフの第一法則と、閉回路における電源の電圧の和は、抵抗の電圧降下の和になるというキルヒホッフの第二法則のことです。

キルヒホッフの法則は非常に優れた理論で使いやすいですが、連立方程式をたてることが多く、計算で解くのに手間がかかってしまうことが解析する回路によってはあります。しかし、これを重ね合わせの理を用いて解くと、もちろん回路によりますが、オームの法則で解析できる場合があるのです。また、重ね合わせの理はよく電流の解析で使用することが多いのですが、電圧の解析においても使用することができる理論です。

ただ、重ね合わせの定理の注意点としては、回路を分離させ分離回路にするときには取り除く電源が電圧源の場合は短絡で、電流源の場合は開放するということです。

つまるところ、デカルト等もいうように困難な問題は分割して考えた方がいいという言葉がよく似合う理論なのが「重ね合わせの理」の勘所です。

重ね合わせの理の例題で学ぶ。電流を求める

これまで、特に電気回路や数式もなく、重ね合わせの理についてを説明してきましたが、ここからは実際に重ね合わせの理を用いた例題を含めて重ね合わせの理の解法手順などについてを紹介します。

重ね合わせの理の例題：電流を求める

問題

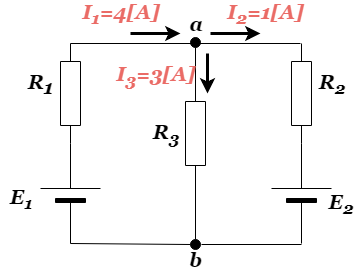
下の図のような回路があるとき、枝電流 $I_1,I_2,I_3$ を求めよ。

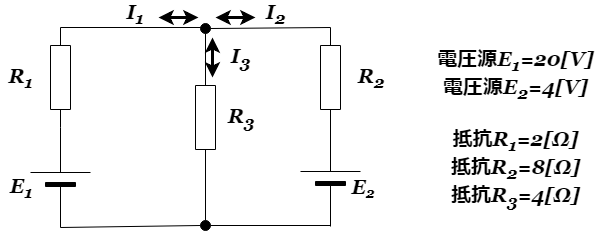
重ね合わせの理の例題・電流を求める

解答手順

①電源ごとに回路を分離する→②分離回路ごとに電流・電圧を解析→③分離回路の電流・電圧を合成という手順で重ね合わせの理を用いて解答していくことができます。

①電源ごとに分離回路を作る

重ね合わせの理を適用する場合、回路に存在する電源の数だけの分離回路をまず作ります。☝の回路図の例題の場合、電源が2つあります。ですので分離回路は2つに分けることができます。どちらも電圧源なので、回路を分離する際にはその部分を短絡処理することで分離させます。

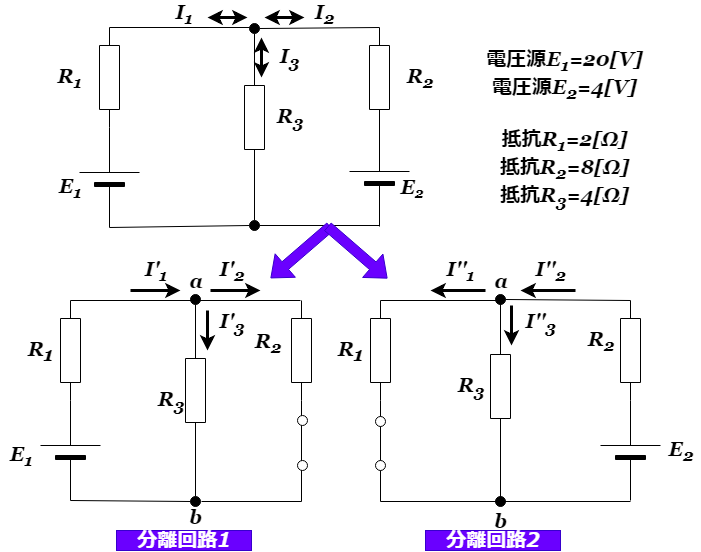
重ね合わせの理の例題の解答の手順その①電源ごとに分離回路を作る

②分離回路ごとに電流を解析する

分離回路を作ったら分離回路ごとに解析を行います。どちらも直並列抵抗回路なので、シンプルにオームの法則を用いて解答していきます。まずは、それぞれの分離回路を変形します。

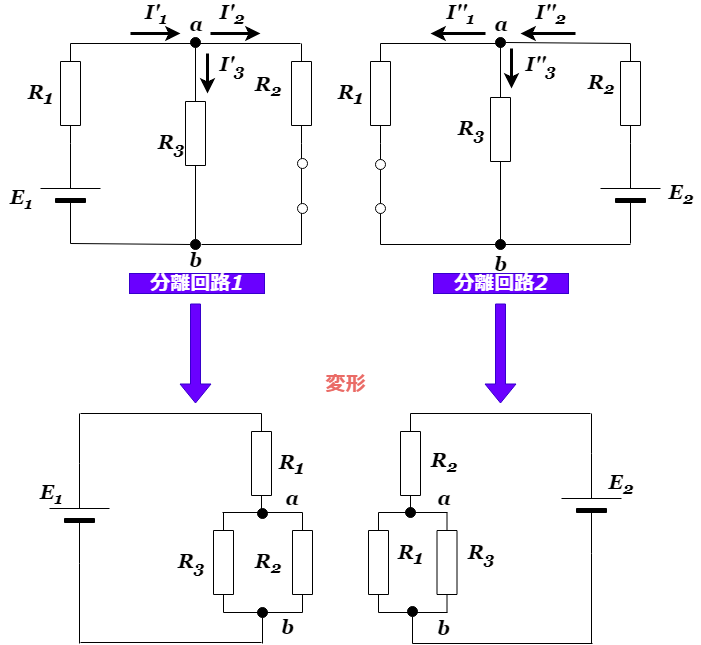
重ね合わせの理の例題の解答の手順②

分離回路1と分離回路2を変形すると☝の図のようになります。分離回路1では、 $R_2,R_3$ の並列接続が抵抗 $R_1$ と直列につながっていることがわかります。ですので、並列接続の部分に和分の積を用いて、合成抵抗と電圧 $E_1$ から枝電流 $I'_1$ を求めることができるようになります。☝の分離回路1は抵抗 $R_2,R_3$ が枝電流 $I'_1$ を分流しているので、分流式によって枝電流 $I'_2,I'_3$ を求めることができます。これは分離回路2も同様です。つまり、分離回路1は分圧式を用いて以下のようになります。(計算過程は省略)

$I'_1=\frac{E_1\left(R_2+R_3\right)}{R_1 R_2+R_1 R_3+R_2 R_3}$

$I'_2=\frac{E_1 R_3}{R_1 R_2+R_1 R_3+R_2 R_3}$

$I'_3=\frac{E_1 R_2}{R_1 R_2+R_1 R_3+R_2 R_3}$

同様に、分離回路2では、以下のようになります。

$I''_2=\frac{E_2\left(R_1+R_3\right)}{R_1 R_2+R_1 R_3+R_2 R_3}$

$I''_1=\frac{E_2 R_3}{R_1 R_2+R_1 R_3+R_2 R_3}$

$I''_3=\frac{E_2 R_1}{R_1 R_2+R_1 R_3+R_2 R_3}$

ここで与えられた数値を代入していくと、次のようになります。

$I'_1=\frac{20\times \left(8+4\right)}{\left(2\times 8\right)+\left(2\times 4\right)+\left(8\times 4\right)}=\frac{30}{7}[A]$

$I'_2=\frac{20\times 4}{\left(2\times 8\right)+\left(2\times 4\right)+\left(8\times 4\right)}=\frac{10}{7}[A]$

$I'_3=\frac{20\times 8}{\left(2\times 8\right)+\left(2\times 4\right)+\left(8\times 4\right)}=\frac{20}{7}[A]$

$I''_1=\frac{4\times 4}{\left(2\times 8\right)+\left(2\times 4\right)+\left(8\times 4\right)}=\frac{2}{7}[A]$

$I''_2=\frac{4\times \left(2+4\right)}{\left(2\times 8\right)+\left(2\times 4\right)+\left(8\times 4\right)}=\frac{3}{7}[A]$

$I'_3=\frac{4\times 2}{\left(2\times 8\right)+\left(2\times 4\right)+\left(8\times 4\right)}=\frac{1}{7}[A]$

③分離回路の電流を合成する

分離回路1と分離回路2の枝電流を求めたら、結果を合成します。重ね合わせの理で得られる計算結果はキルヒホッフの法則で解く結果と同一です。また、分離前の回路で方向を枝電流を仮定していれば、分離回路の枝電流が同じ方向のものを＋、逆方向のものを⁻となることがわかります。結果的に問題・例題の解答は以下のようになります。

重ね合わせの理の例題の解答・合成抵抗

$I_1=I'_1-I''_1=\frac{30}{7}-\frac{2}{7}=4[A]$

$I_2=I'_2-I''_2=\frac{10}{7}-\frac{3}{7}=1[A]$

$I_3=I'_3+I''_3=\frac{20}{7}-\frac{1}{7}=3[A]$

電気回路を解析するにあたって、重ね合わせの理は非常にシンプルな理論で、回路の変形図を描かなくても慣れてくれば頭の中で回路を組み立てることができるようになります。

重ね合わせの理を使用し、電圧を解析する

先ほどの項では、重ね合わせの理を用いて電気回路の電流を解析してきました。次に、解析対象の回路の各抵抗の電圧降下は、解析した枝電流と既知の抵抗から算出できます。ここで、重ね合わせの理を電圧を求める場合で使用した場合についてを先ほどの回路を使用し、解説していきます。

重ね合わせの理：電圧降下

左側の回路を分離回路1、右側の回路を分離回路2として、それぞれの電圧の値を求めると、分離回路1では、

$V'_1=I'_1 R_1=\frac{60}{7}[V]$

$V'_2=I'_2 R_2=\frac{80}{7}[V]$

$V'_3=I'_3 R_3=\frac{80}{7}[V]$

となります。同様に、分離回路2の電圧を求めると、以下のようになります。

$V''_1=I''_1 R_1=\frac{4}{7}[V]$

$V''_2=I''_2 R_2=\frac{24}{7}[V]$

$V''_3=I''_3 R_3=\frac{4}{7}[V]$

となります。分離回路の電圧降下はこのようになりますが、電圧降下の場合、合成の際の方向は分離回路の電圧降下の大きさで判断することができるようになります。ここでの解析に当たってもキルヒホッフの法則を用いて電圧を求めることができます。

重ね合わせの理：電圧降下の合成抵抗

電流源と電圧源が混在している複雑な回路の重ね合わせの理

重ね合わせの理を用いた電気回路の解析においては電圧源と電流源は異なる扱いをします。ここでは、重ね合わせの理を用いた電圧源と電流源が混在している電気回路の解析を電流源と電圧源がある回路で電流を求める例題と併せて解説します。解析対象として下のような電気回路があるとします。

重ね合わせの理：電流源と電圧源が混在する回路の例題

この電圧源と電流源が混在している電気回路において、枝電流 $I_1,I_2,I_3$ を求めます。先ほどの電気回路とは異なり、今回は電流源がある電気回路です。この回路を同様に電圧源と電流源に分けて分離回路を作ります。その時に注意点として、電圧源を残す分離回路では、電流源の部分は開放します。ですので抵抗 $R_2$ には電流が流れません。分離回路を作成し、わかり安いように変形すると、以下のようになります。

重ね合わせの理：電流源と電圧源が混在する回路の変形

このとき、☝の電気回路の左を分離回路1’、右の分離回路を2’とすると、分離回路1’は以下のように枝電流 $I'_1,I'_2,I'_3$ を求めることができます。

$I'_1=I'_3=\frac{E}{R_1+R_3}=\frac{20}{12+4}=\frac{5}{4}[A]$

つまり、分離回路1’では、抵抗 $R_1,R_3$ の合成抵抗と電圧源Eで求めることができ、 $R_2$ を開放しているので、枝電流 $I'_2$ はゼロとなります。次に、分離回路2’を求めていきます。分離回路2’は変形した上の回路を見ればわかるように、抵抗 $R_1$ を流れる電流 $I''_1$ と $R_3$ を流れる電流 $I''_3$ は $I$ を分流しています。ですので、分流式を用いて計算していきます。

$I''_1=\frac{R_3}{R_1+R_3}=\frac{4}{12+4}=\frac{1}{4}[A]$

$I''_3=I''_2\frac{R_1}{R_1+R_3}=\frac{12}{12+4}=\frac{3}{4}[A]$

それぞれの分離回路の枝電流を求めたところで、それらを合成していきます。この手順に関しては先ほどの電気回路の解析と同様です。つまり、以下のようになります。

$I_1=I'_1-I''_1=\frac{5}{4}-\frac{1}{4}=1[A]$

$I_3=I'_3+I''_3=\frac{5}{4}+\frac{3}{4}=2[A]$

重ね合わせの理：電流源と電圧源が混在する回路端子電圧を求める

枝電流を求めることができたので、次に電流源 $I$ の端子電圧 $E_1$ を求めます。各抵抗の電圧降下を求めればいいので、節点bを基準とすると、節点aの電圧 $V_a$ は抵抗 $R_3$ の電圧降下 $V_3$ から次のように求めることができます。

$V_a=V_3=I_3 R_3 =2\times 4~8[V]$

$V_a=E_1-V_2=E_1-I_2 R_2=E_1-1\times 8=8[V]$

となります。

交流回路における重ね合わせの理

これまで、直流回路において、重ね合わせの理を適用して電流や電圧を求めてきましたが、重ね合わせの理は直流回路だけでなく、交流回路においても適用することができる解析方法です。次に交流回路においての重ね合わせの理を用いた解析を解説していきます。

複数の電源がある回路の解析においては重ね合わせの理も記号法ならば交流回路においても適用することが可能になります。プロセスは直流回路と同様に、電源ごとに回路を解析していき、最後に合成するのです。

交流回路の重ね合わせの理は「回路に複数の電源があるとき、回路の任意の点の電流及び電圧のフェーザは、それぞれの電源が単独で存在した場合のフェーザの和に等しい」と考えることができます。つまり、1つだけ電源を残した分離回路ごとに解析し、最後に合成すればよいのです。交流回路における重ね合わせの理においての注意点として、取り除く電源が電圧源の場合は短絡、電流源の場合は開放するという点です。実際に交流回路で重ね合わせの理を用いた解法を取る例題を以下に示します。

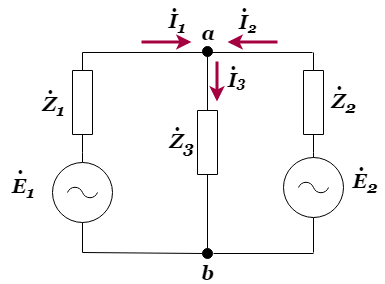
重ね合わせの理を用いた交流回路の解析の例題

この交流回路において、枝電流 $\dot{I_1},\dot{I_2},\dot{I_3}$ えお求めます。まず、電源 $\dot{E_1}$ を残し、電圧源である $\dot{E_2}$ を短絡した分離回路1”を以下のように作ります。同様に分離回路2”も作ります。

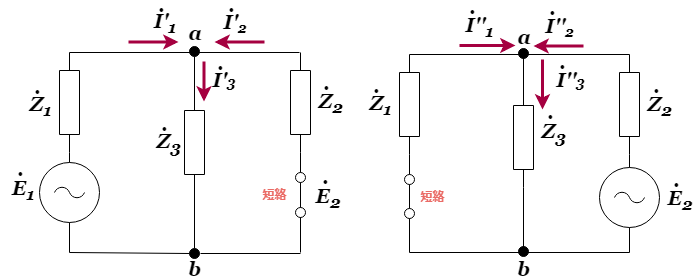
重ね合わせの理を用いた交流回路の分離回路

まずは、☝の回路の左側の分離回路1”についてを見ていきます。計算方法は、並列接続の $\dot{Z_2}$ と $\dot{Z_3}$ を和分の積を用いて計算します。そこに直列接続の $\dot{Z_1}$ を加えて合成インピーダンスから $\dot{I'_1}$ を求めることができます。 $\dot{I'_2},\dot{I'_3}$ に関しては、 $\dot{I'_1}$ から分流式を用いて求めることができます。

$\dot{I'_1}=\frac{\dot{E_1}}{\dot{Z_1}+\left(\frac{\dot{Z_2}\dot{Z_3}}{\dot{Z_2}+\dot{Z_3}}\right)}$

$=\frac{\dot{E_1}\left(\dot{Z_2}+\dot{Z_3}\right)}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

$\dot{I'_2}=-\dot{I'_1}\frac{\dot{Z_3}}{\dot{Z_2}+\dot{Z_3}}=-\frac{\dot{Z_1}\dot{E_1}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

$\dot{I'_3}=\dot{I'_1}\frac{\dot{Z_2}}{\dot{Z_2}+\dot{Z_3}}=\frac{\dot{E_1}\dot{Z_2}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

となります。同様にして、☝の回路図の右側の分離回路2”についても枝電流 $\dot{I''_1},\dot{I''_2},\dot{I''_3}$ を求めていきます。

$\dot{I''_2}=\frac{\dot{E_2}}{\{Z_2}+\left(\frac{\dot{Z_1}\dot{Z_3}}{\dot{Z_1}+\dot{Z_3}}\right)}$

$=\frac{\dot{Z_2\left(\dot{Z_1}+\dot{Z_3}\right)}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

$\dot{I''_1}=-\dot{I''_2}\frac{\dot{Z_3}}{\dot{Z_1}+\dot{Z_3}}=-\frac{\dot{E_2}\dot{Z_3}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

$\dot{I''_3}=\dot{I''_2}\frac{\dot{Z_1}}{\dot{Z_1}+\dot{Z_3}}=\frac{\dot{E_2}\dot{Z_1}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

となります。それぞれの分離回路の枝電流を求めると、後は枝電流を加算するだけでよく、この結果はキルヒホッフの法則で得られる結果となります。次のようになります。

$\dot{I_1}=\dot{I'_1}+\dot{I''_1}\\&=\frac{\dot{E_1}\left(\dot{Z_2}+\dot{Z_3}\right)-\dot{E_2}\dot{Z_3}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

$\dot{I_2}=\dot{I'_2}+\dot{I''_2}\\&=\frac{\dot{E_2}\left(\dot{Z_1}+\dot{Z_3}\right)-\dot{E_1}\dot{Z_3}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

$\dot{I_3}=\dot{I'_3}+\dot{I''_3}\\&=\frac{\dot{E_1}\dot{Z_2}+\dot{E_2}\dot{Z_1}}{\dot{Z_1}\dot{Z_2}+\dot{Z_1}\dot{Z_3}+\dot{Z_2}\dot{Z_3}}$

まとめ

以上のように、電気回路を解析するうえで重要な知識である重ね合わせの理についてを直流回路と交流回路、電流源、電圧源が混在する回路などから解説してきました。

はじめは重ね合わせの理を使えると思った回路でもどのように変形して計算式を組み立てていけばわからないということはよくあります。しかし、重ね合わせの理を用いて電気回路を解析していけばいずれ慣れて、頭の中で回路の変形ができるようになります。そうすると、その分正確性が求められはしますが、回路を解析するスピードも速くなります。

ここまでお読みいただきありがとうございました。
この記事が皆さんの理解に役立ちましたら幸いです。