[水力発電]水車の比速度の意味、式や問題について

水車は、水源の落差や流量によって、大きさや形状が異なることがあります。ランナ形状が幾何学的に相似ならば、ランナの寸法に関係なく、ほぼ同様の特性を有します。そのために、大容量の水車を設計・製造する場合において、小型の相似形のモデルを試作することで問題がないかどうかを確認する手法はよく取られています。

水車の比速度は、水車の特性を推測するための指標となっています。小型相似形水車の比速度によって、設計する水車の特性を推測することができるのです。この記事では、水力発電に使用する水車の比速度の定義や式、問題例などについてを紹介します。

1 [水力発電]水車の比速度とは？定義
2 [水力発電]水車の比速度の式・覚え方
3 [水力発電]水車の比速度を求める問題
4 まとめ

[水力発電]水車の比速度とは？定義

水車の比速度とは？

水車の比速度は前述の通り、水車の特性を推測するための指標となっています。水車の比速度は、水車と相似な水車を仮定し、これを単位落差(1m)の下で相似な状態で運転させます。そして、単位出力1kWを発生させたときの1分間当たりの回転数 $min^{-1}$ を言います。比速度の単位としては、落差[m]と出力[kW]で計算した比速度という意味で一般的に[mkW]が使用されています。

つまり、水車の比速度とは水車の種類に応じてその能力を比較するために、単位高さ・単位出力当たりの回転速度を求めることに他なりません。水車の比速度の仕組みを覚えやすいように図で示すと以下のようになります。

比速度が大きくなると、発電機や水車を小型化することが可能になります。そのため、建設費用を低減できるので、経済的です。ですが、流水とランナの相対速度が増大するので効率低下やキャビテーション発生、振動・騒音などの問題が生じる可能性があります。相対速度というのは、運動している2つの物体のお互いの速度差のことを表しています。

[水力発電]水車の比速度の式・覚え方

水車の比速度の式

水力発電の水車の比速度の式は以下のようになります。

$N_s=N\frac{P^{\frac{1}{2}}}{H\frac{5}{4}}[mkW]....(1)$

ここで、 $N_s$ :比速度、 $P$ :ペルトン水車の場合はノズル1個当たりの出力(kW)、反動水車ではランナ1個当たりの出力[kW]、 $N$ :回転速度( $min^{-1}$ )、 $H$ :有効落差(m)を指します。

上の比速度の式は一見覚えにくい式のように見えますが、文章に落とし込むと少し覚えやすいかと思われます。つまり、比速度は出力の $\frac{1}{2}$ 乗に比例し、有効落差の $\frac{5}{4}$ 乗に反比例します。出力が大きな水車ほど比速度が大きくなり、有効落差が大きい場合は比速度が小さくなることを示している式ともいえます。

水車の比速度の式の証明

水車の比速度の式は☝の(1)式のようになることがわかりましたが、どのように算出できるのかを証明していきます。まず、力学的エネルギー保存の法則によって次の関係式が成り立ちます。mgHは位置エネルギーを示します。このことは水力発電の仕組みの記事でも説明しています。

$\frac{1}{2}mv^2=mgH$

この関係式より、 $H \varpropto v^2$ となります。∝は比例関係を示しています。

回転速度Nとvの関係において、単位をmで統一すると、以下のようになります。

$2\pi r \cdot t \cdot N=v\cdot t$

$v\varpropto N\cdot r$

ゆえに、

$H\varpropto N\cdot r^2$

流量 $Q[m^3/s]$ は、以下のようになります。

$Q\varpropto \pi r^2\cdot v \varpropto r^2Nr \varpropto Nr^3$

ここで、2つの相似形ランナとノズルを考慮すると、以下のようになります。

$\frac{Q'}{Q}=\left(\frac{N'}{N}\right)\left(\frac{r'}{r}\right)^3$

$\frac{r'}{r}=\left(\frac{N'}{N}\right)^{-\frac{1}{3}}\left(\frac{Q'}{Q}\right)^{\frac{1}{3}}$

$\frac{H'}{H}=\left(\frac{N'}{N}\right)^2\left(\frac{r'}{r}\right)^2$

$\frac{r'}{r}=\left(\frac{N'}{N}\right)^{-1}\left(\frac{H'}{H}\right)^{\frac{1}{2}}$

したがって、

$\left(\frac{N'}{N}\right)^{-1}\left(\frac{H'}{H}\right)^{\frac{1}{2}}=\left(\frac{N'}{N}\right)^{-\frac{1}{3}}\left(\frac{Q'}{Q}\right)^\frac{1}{3}$

となります。これを整理すると、

$\frac{N'}{N}=\left(\frac{H'}{H}\right)^{\frac{1}{2}}\left(\frac{Q'}{Q}\right)^{-\frac{1}{3}}$

$N'\frac{Q'^{\frac{1}{2}}}{H'^{\frac{3}{4}}}=N\frac{Q^{\frac{1}{2}}}{H^{\frac{3}{4}}}=N_s$

となります。この式が比速度の式になっていることがわかります。ここで、 $P=9.8QH$ となり、

$Q \varpropto \frac{P}{H}$

したがって、以上より、

$N_s=N\times \frac{P^{\frac{1}{2}}}{H^{\frac{5}{4}}}$

となります。この式が水車の比速度を表している式になることがわかります。

主な水車の種類別比速度と適用落差との関係

主な水車の種類(ペルトン水車、フランシス水車、プロペラ水車)と適用落差の関係を☟の図にしめします。

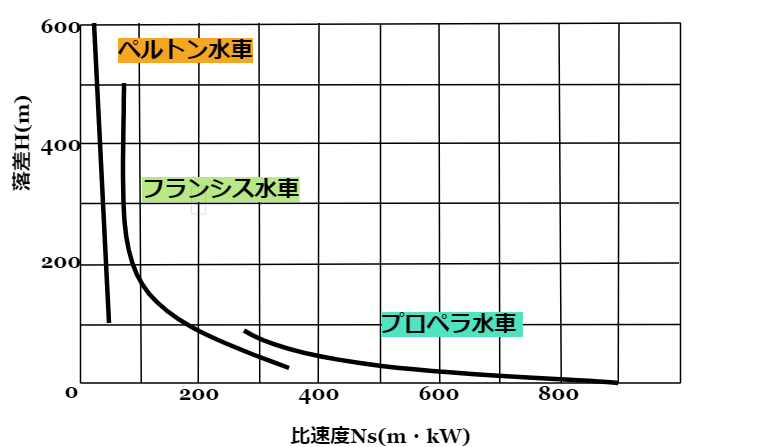
水力発電の水車の比速度

この図からわかるように、ペルトン水車は適用落差が高く、比速度が小さいです。一方、プロペラ水車は適用落差が低く、比速度大きいという特徴を持っています。比速度と適用落差には反比例の関係があることがわかります。水力発電のそれぞれの水車の比速度の下限と上限や特徴は以下のようになります。

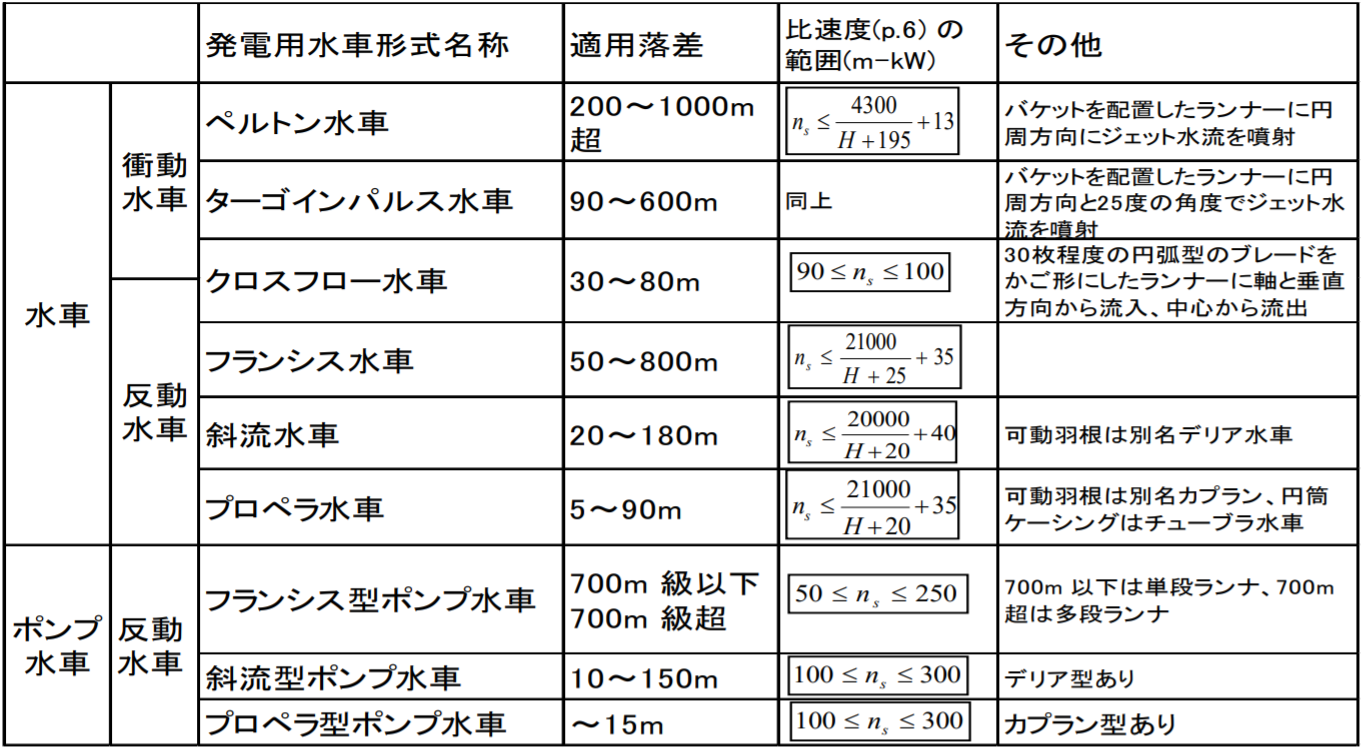
水車比速度上限(水車の比速度お上限:出典:宮田明則技術士事務所)

[水力発電]水車の比速度を求める問題

電験三種電力H21の過去問より水車の比速度を求める計算問題

問題

有効落差256[m]、最大使用水量11.5[m3/s]、周波数60[Hz]の水力発電所がある。
水車としての効率86[%]の6ノズルペルトン水車を採用したとき、比速度は22.6[m・km]となった。このときの回転速度[rpm]はいくらか。

解答例

まず、この水車の出力P[kW]は有効落差に流量の積で求まるので、以下のように求めることができます。

$P=9.8\times 256\times 11.5\times 0.86=24,812[kw]$

題意より、この水車のノズルは6ノズルのペルトン水車ですので、1台のノズル分の出力は以下のように求めることができます。

$\frac{24,812}{6}=4,135[kW]$

ここで、水車の比速度の式を用いると、

$N_s=N\frac{P^{\frac{1}{2}}}{N^{\frac{5}{4}}}$

となるので、

$22.6=\frac{N\sqrt{4,135}}{256^{\frac{5}{4}}}$

したがって、

$N=\frac{22.6\times 256^{\frac{5}{4}}}{\sqrt{4,135}}=360[rpm]$

となり、問題の解答は360[rpm]となります。電験三種の電力の問題では水車の比速度に関しての計算問題が出題されることもありますし、穴埋め形式で出題されることもあります。いづれにせよ過去問から傾向を掴むことができます。

まとめ

以上のように、水力発電の水車の比速度の意味や照明、水車毎の上限比速度、比速度の問題などについてを紹介してきました。水車の比速度は水力発電の発電において重要な指標となっています。その意味や式については押さえておく必要があるでしょう。