PID制御とは？ゲイン設計ってどうやるの？

制御工学におけるフィードバック制御の１つであるPID制御について紹介します。PID制御は実用的にもよく使われる手法で、ロボットのライントレース制御や温度制御、モータ制御など様々な用途で利用されています。また、電験３種、電験２種（機械・制御）に出題されることがあります。

自動制御、PID制御、フィードバック制御とは？

自動制御とは目標値を実現するために自動的に入力量を調整すること

「制御」とは目標値に測定値を一致させることであり、「自動制御」はセンサーなどの値も利用して自動的にコントロールすることを言います。フィードバック制御はまさにこのセンサーを利用（フィードバック）させることで測定値を目標値に一致させることを目的とします。単純な制御として「オン・オフ制御」があります。これは文字通り、とあるルールに従ってオンとオフの２通りで制御して目標値に近づける手法です。この制御方法では、0%か100%でしか操作量を制御できないため、オーバーシュートやハンチングが発生しやすいデメリットがあります。PID制御はP（Proportional:比例)動作、I（Integral：積分）動作、D（Differential :微分）動作の３つの要素があります。それぞれの特徴を簡潔に示します。

P（比例）動作：　　目標値とフィードバック値の偏差の比例値を操作量とします。安定した制御はできますが、偏差が小さくなると操作量が小さくなっていくため、目標値はフィードバック値に完全に一致せず、オフセット（定常偏差）が残ります。

I（積分）動作：　　目標値とフィードバック値の偏差の積分値を操作量とする。偏差があると、積算されて操作量が大きくなっていくためP制御のようなオフセットは発生しません。ただし、制御系の遅れ要素となるため、制御を不安定にする場合があります。

D（微分）動作：　　目標値とフィードバック値の偏差の微分値を操作量とします。偏差の変化量に比例した操作量を出力するため、制御系の進み要素となり、制御応答の改善につながります。ただし、振動やノイズなどの成分を増幅し、制御を不安定にする場合があります。

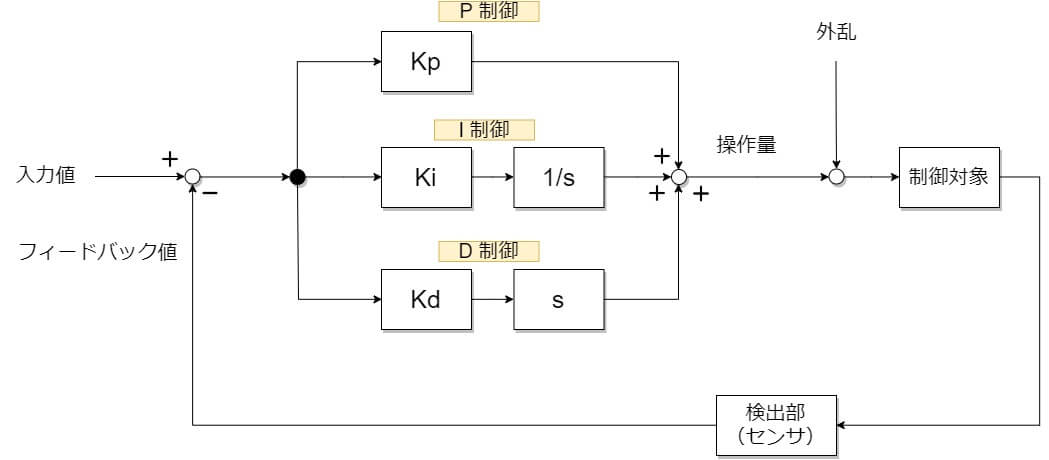
PID制御のブロック線図を上に示します。「入力値（目標値）」と「フィードバック値」を一致させる役割を担うのがPID制御器です。PIDそれぞれの制御のゲインをKp, Ki, Kdと表記しています。1/sは積分を、sは微分を示します。ゲインの大きさによって目標値に素早く収束させたり、場合によっては制御が不安定になって発振してしまうこともあります。したがって、制御対象のシステム特性に応じて適切にゲインを設定することが実用上重要です。

それでは、電気回路（RL回路）における電流制御を例に挙げて、PID制御を見ていきます。電流制御といえば、モータのトルクの制御などで利用されていますね。モータの場合は回転による外乱（誘起電圧）等があり、制御モデルはより複雑になります。

PID制御で電気回路の電流を制御してみよう

RL回路において電流を制御する

シンプルなRLの直列回路において、目的の電流値（Iref）になるように電圧源（Vc）を制御してみましょう。電流検出器で電流値Idet（フィードバック値）を取得します。「制御器」はIrefとIdetを一致させるようにPID制御する構成となっており、操作量が電圧指令（Vref）となります。Vref通りに電圧源の出力電圧を操作することで、出力電流値が制御されます。

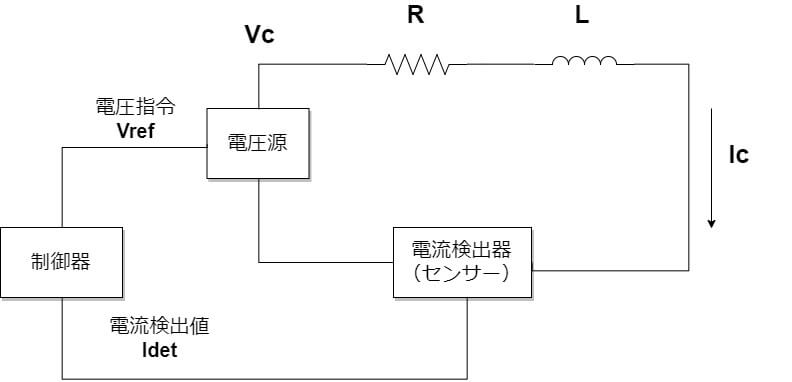
RとLの直列回路は上記回路を制御ブロック図に当てはめると以下の図となります。ここで、「電圧源」と「電流検出器」がブロック図に含まれていますが、これは省略しても良いのでしょうか？　現実的には「電圧源」は電圧指令が入ったら瞬時にその電圧を出力してくれるわけではありません、「電圧源」も電気回路で構成されており、電圧は指令より遅れて出力されます。電流検出器も同様に遅れます。しかし、制御対象となるRL直列回路に比べて無視できるほどの遅れであれば伝達特性を「１」と近似でき、ブロックを省略できます。

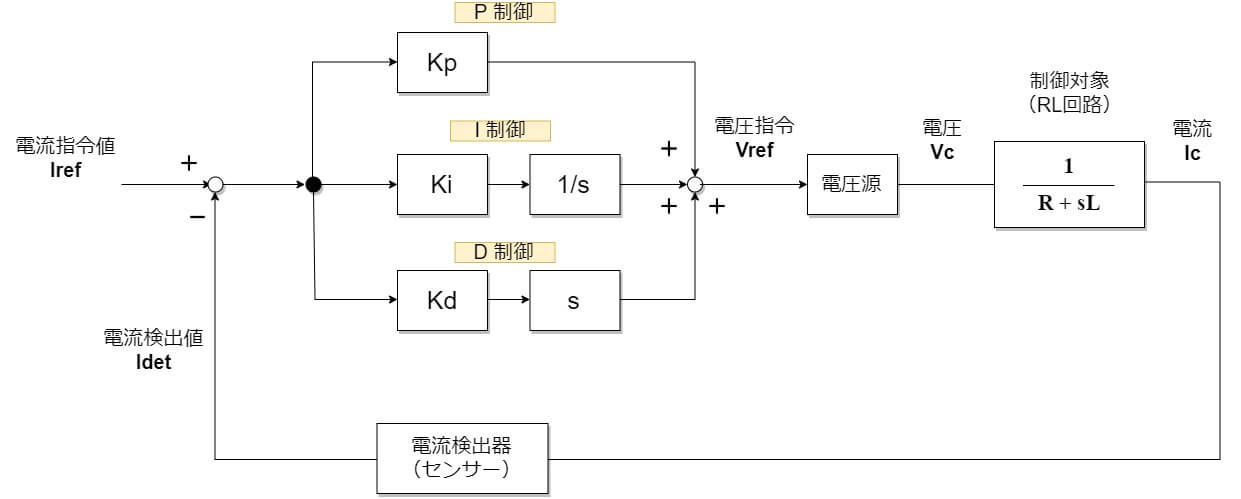
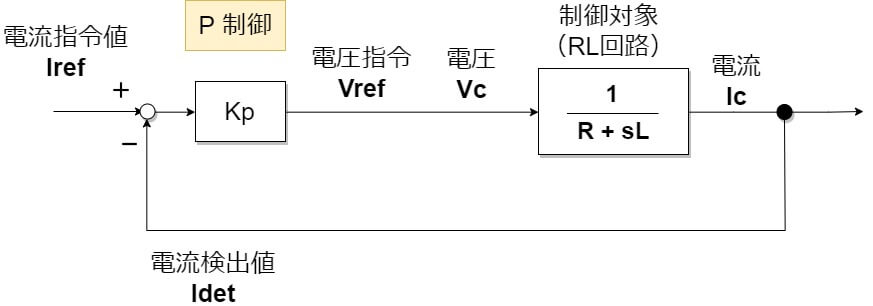
P制御

KiとKdを０、すなわちI制御、D制御を無効にしてP制御のみ動作させてみます。制御ブロックは以下となります。

システムの入力Iref(s)から出力Ic(s)までの伝達関数を解いてみます。

$\begin{align*} I_{c}(s) &= \frac{K_p}{R + sL} (I_{ref}(s)-I_{c}(s) ) \\\\ (1+\frac{K_p}{R + sL})I_{c}(s) &= \frac{K_p}{R + sL} I_{ref}(s) \\\\ I_{c}(s) &= \frac{K_p}{(R + K_p) + sL}I_{ref}(s) \end{align*}$

これはRL回路の伝達関数と同じく１次フィルタ（ローパスフィルタ）の形になっていますね。ここで、R=1.0[Ω]、L=0.1[H]、として、Iref=1.0[A]のステップ入力を入れて出力電流Idet[A]をみてみましょう。P制御ゲインはKp=1.0(青）、5.0（赤）の２通りでシミュレーションします。

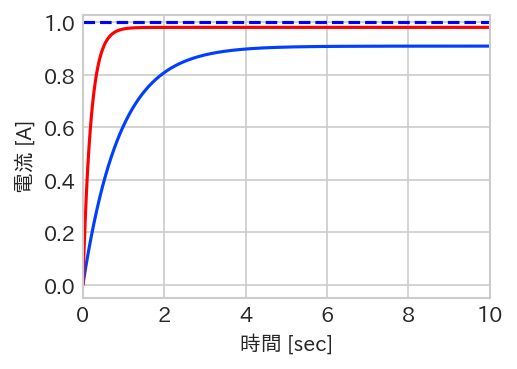
Kp=5.0のほうがより収束が早く、Iref=1.0[A]に近い値に収束していますね。しかし、Kp=1.0、5.0どちらも「定常偏差」が残っております。この値は、伝達関数のsを0（言い換えると、直流成分（周波数0Hz））とおくことで以下のように最終的な収束値がわかります。

$I_{c}(s) = \frac{K_p}{R + K_p}I_{ref}(s)$

Kp→∞とすると伝達関数が１に収束していきますね。そこで、Kp = 30としてみます。

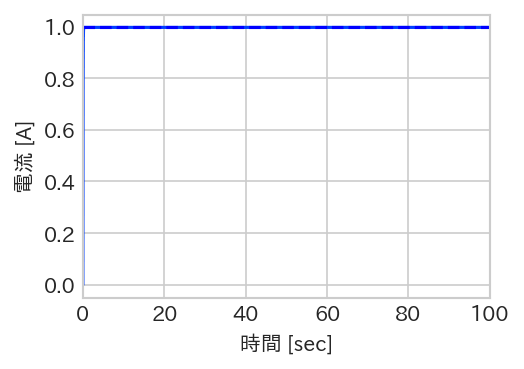
Idetがほとんど一瞬で目的の1.0[A]になりました。ただし、Kpを大きくするということは電圧指令値も大きくなるということになります。電圧源が実際に出力できる電圧は限界があるため、現実的にはKpを無限に大きくすることはできません。

I制御

それでは、P制御の「定常偏差」を解決するI制御をみていきましょう。

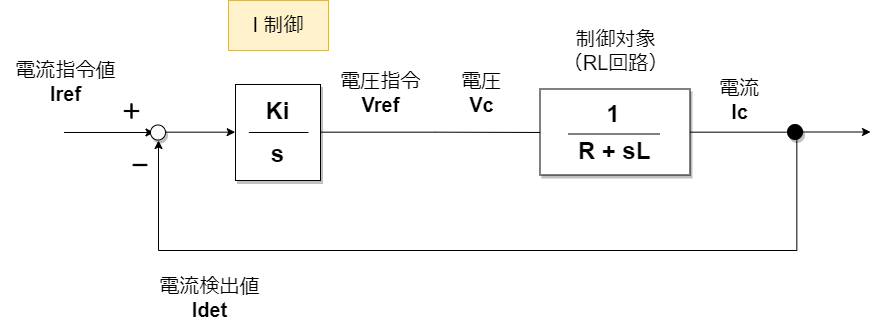
伝達関数は次の通りです。

$\begin{align*} I_{c}(s) &= \frac{K_i}{s(R + sL)} (I_{ref}(s)-I_{c}(s) ) \\\\ (1+\frac{K_i}{s(R + sL)})I_{c}(s) &= \frac{K_i}{s(R + sL)} I_{ref}(s) \\\\ I_{c}(s) &= \frac{K_i}{s^2L+sR + Ki}I_{ref}(s) \end{align*}$

これは２次系の伝達関数となっていますね。２次系のシステムは、ωn:固有角周波数、ζ:減衰比などでその振動特性を表現でき、制御ではよく現れる特性です。

2次系の伝達関数

$G(s)=\frac{\omega_n^2}{s^2+2\zeta\omega_n s+1}$

さて、回路は同じ条件（R=1.0[Ω]、L=0.1[H])とし、Ki = 0.1（青）、2.0（赤）の２通りでシミュレーションしてみます。

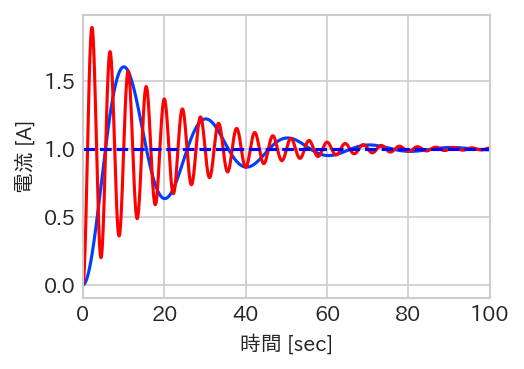
100秒ほど経過すると、値が1.0[A]に収束していくことが確認できますね。しかし、電流値Idetは物凄く振動してます。このような振動は発熱を起こしたり、機器の破壊の原因になったりするので実用上はよくありません。I制御のみで制御しようとすると、不安定になりやすいことが確認できました。

D制御

微分に応じて操作量を変化させるD制御をみてみましょう。

D制御のみでの伝達関数は次の通りです。

$\begin{align*} I_{c}(s) &= \frac{sK_d}{R + sL} (I_{ref}(s)-I_{c}(s) ) \\\\ (1+\frac{sK_d}{R + sL})I_{c}(s) &= \frac{sK_d}{R + sL} I_{ref}(s) \\\\ I_{c}(s) &= \frac{sK_d}{s(L+K_d) + R}I_{ref}(s) \end{align*}$

Kd = 1.0（青）, 10.0（赤）の２通りでシミュレーションしてみます。

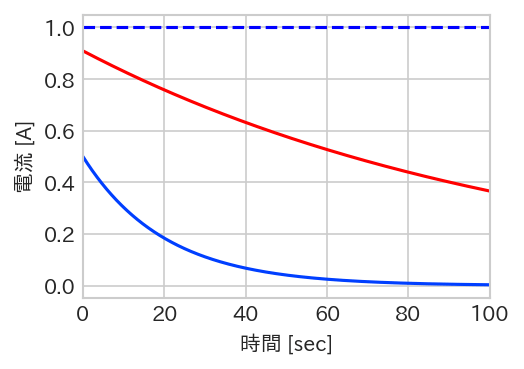
ステップ応答立ち上がりの0 [sec]時に急激に電流が立ち上がり、その後は徐々に電流が減衰しています。これは、0 [sec]のときIrefがステップで立ち上がることから直感的にわかりますね。時間が経過して電流の変化が緩やかになると、偏差の微分値は小さくなるため減衰していきます。伝達関数の分子のsに0を入れると、出力電流Idetは0になることからも理解できます。

PI制御

P制御のデメリットである「定常偏差」を、I制御と一緒に利用することで克服することができます。制御ブロック図は省略します。以下は伝達関数式です。

$\begin{align*}I_{c}(s) &= \frac{K_p+\frac{K_i}{s}}{R + sL} (I_{ref}(s)-I_{c}(s) ) \\\\ &= \frac{\frac{K_p+\frac{K_i}{s}}{R + sL}}{1+\frac{K_p+\frac{K_i}{s}}{R + sL}}I_{ref}(s)\\\\ &=\frac{K_p+\frac{K_i}{s}}{R+sL+K_p+\frac{K_i}{s}}\\\\ &=\frac{sK_p+K_i}{s^2L+s(R+K_p)+K_i} \end{align*}$

式において、s=0とおくと伝達関数は「1」になるので、目標値とフィードバックは最終的に一致することが確認できます。それでは、Kp=5.0, Ki=1.0 (青）と、Kp=5.0, Ki = 10.0（赤）の場合でステップ応答をシミュレーションしてみましょう。

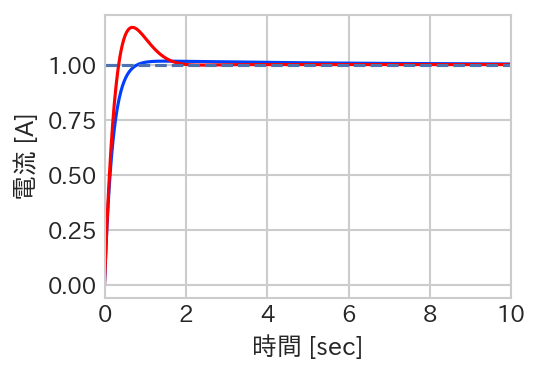
2秒後にはほとんど一致していますね。応答も早く、かつ「定常偏差」を解消することができています。

制御を安定させつつ応答を上げたい、PIDのゲイン設計はどうしたらよい？

RL直列回路のように簡素な制御対象であれば、伝達特性の数式化ができるため、希望の応答になるようなゲインを設計することができます。しかし、実際の制御モデルは複雑であるため、モデルのシミュレーションや、実機でゲインを調整して最適値を見つけていくことが多いです。よく知られている調整手法としては、調整したゲインのテーブルを利用する限界感度法や、ステップ応答曲線を参考にするCHR法などがあります。制御システムによっては、PID制御器を複数もつような場合もあり、制御器同士の干渉が無視できないことも多くあります。ここまで複雑になると、最終的には現場の技術者の勘に頼った調整になる場合もあるようです。

PID制御は「フィードバック制御」の一つと冒頭でお話いたしましたが、「フィードフォワード制御」などもあります。これは制御のモデルが既知の場合はセンサーなどを利用せず、モデル式から前向きに操作量に足し合わせる方法です。フィードフォワード制御は遅れ要素がなく、安定して制御応答を向上することができます。ここで例に挙げたRL直列回路では、RとLの値が既知であれば、電圧から電流を得ることができ、この電流から必要となる電圧を計算するようなイメージです。ただし、フィードフォワード制御だけでは、実際値の誤差を修正することはできないため、フィードバック制御との組み合わせで用いられることが多いです。

連続モデルと離散モデル

本記事ではPID制御器の伝達関数をs（連続モデル）として考えました。しかし、現実の制御器はアナログな回路による制御以外にもCPUなどを用いたデジタルな制御も数多くあります。この場合、z変換（離散モデル）で伝達特性を考えたほうがより正確に制御できる場合があります。ｓ領域とｚ領域の関係は以下式より得られます。Tはサンプリング時間です。

(1) $\begin{align*} z &= e^{Ts}\\ s &=\frac{1}{T}\ln (z) \end{align*}$

指数関数では計算が大変なので、大抵は近似式を利用します。1次近似式（前進差分式）は次のようになります。

$s \approx \frac{z-1}{T}$

シミュレーションコード（python）

ステップ応答の描画にpython control systems libraryを利用しました。以下にPI制御の応答を出力するコードを載せておきます。

import numpy as np
from numpy.random import *
from control import matlab
from matplotlib import pyplot as plt
from pylab import *
import matplotlib.pyplot as plt
plt.style.use('seaborn-bright')

fig = plt.figure(figsize=(3.5,2.5),dpi=150)
plt.grid()

# 制御対象(RL回路)
R = 1.0
L = 0.1
num = [1.0]
den = [R, L]
G = matlab.tf(num, den)

# time array
t = np.arange(0, 100, 0.01)

# PI gain 1
Kp = 5.0  
Ki = 1.0 

num = [Kp,Ki]
den = [1,0]
K1 = matlab.tf(num, den)
sys1 = matlab.feedback(K1*G, 1)

(y1, T1) = matlab.step(sys1, T = t)
plt.plot(T1, y1)

# PI gain 2
Kp=5.0
Ki=10.0
num = [Kp,Ki]
den = [1,0]
K2 = matlab.tf(num, den)
sys2 = matlab.feedback(K2*G, 1)

(y2, T2) = matlab.step(sys2, T=t)
plt.plot(T2, y2, color="red")

plt.axhline(1, color="b", linestyle="--")
plt.xlim(0, 10)
plt.xlabel('時間 [sec]')
plt.ylabel('電流 [A]')

plt.grid()
plt.show()