三相交流回路で多様されることがあるのがΔ結線とY結線ですが、相互の等価変換を活用することで複雑な回路の解析を簡単に行うことができるようになるのです。Δ-Y変換は第三種電気主任技術者試験(電験3種)の理論の問題でもしばしば出題されるほど重要な電気回路の解析方法です。

Δ-Y変換とは?直流回路
直流回路においてΔ結線とY結線は相互変換可能
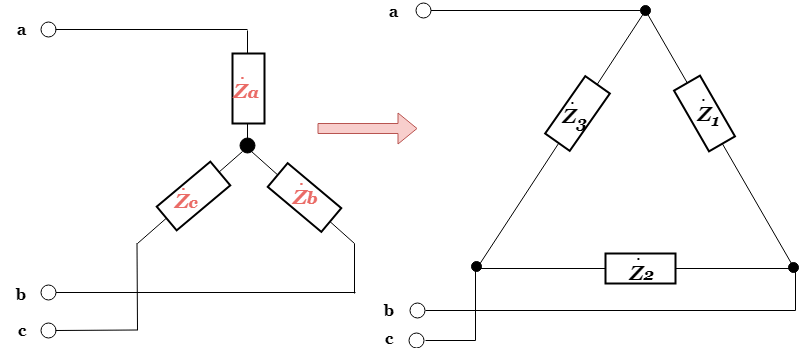
下の図左のような素子の接続をΔ結線やΔ接続といい、図右のような素子の接続をY結線やY接続といいます。この2種類の結線は相互に等価変換することができるのです。このようなΔ-Y結線は三相交流回路でしばしば用いられます。この等価回路を利用することによってオームの法則では解析できない複雑な回路も解析が可能になるのです。
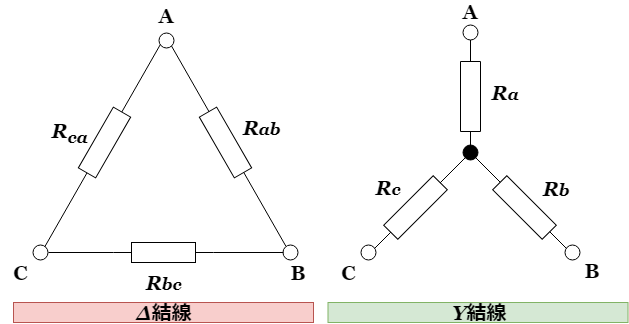
Δ結線とY結線が等価であるための条件としては、☝の図の双方の結線で端子A-B間、端子B-C間、端子C-B間の抵抗の大きさが同一である必要があります。Δ結線をY結線に変換するには次のような公式を使用します。
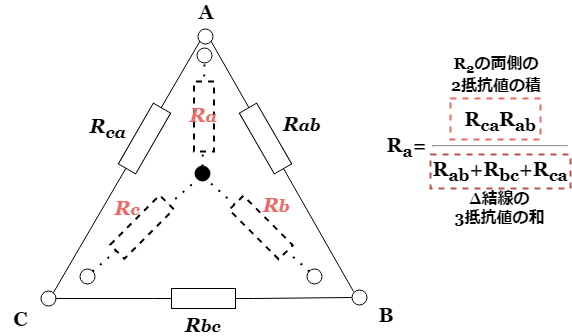
Δ-Y変換の公式は、和文の積で理解することが可能です。
![]()
![]()
![]()
![]()
ここで、![]() を求めるには、次の式のように分母はΔ結線の3個の抵抗値の和、分子は
を求めるには、次の式のように分母はΔ結線の3個の抵抗値の和、分子は![]() の両側の2個の抵抗値の和になります。
の両側の2個の抵抗値の和になります。
Δ-Y変換とY-Δ変換:三相交流回路
三相交流回路において、負荷にΔ回路とY回路の両方がある場合、いずれかの回路に統一して計算を行うことができます。
三相交流回路におけるΔ→Y変換
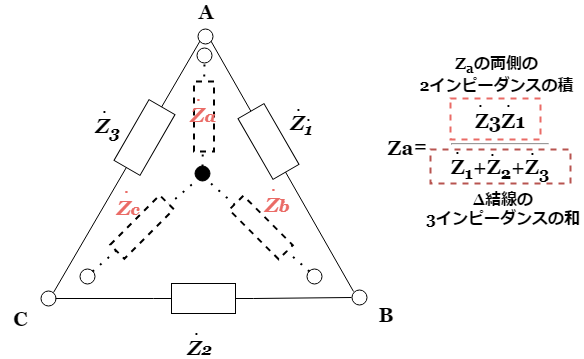
Δ回路をY回路に変換するには、変換公式を使用することで計算が可能になります。直流回路と同様に、三相交流回路においてもΔ-Y変換は和分の積を使用します。交流でもΔ-Y変換は可能で、三相交流回路の解析では必須の理論となります。
![]()
![]()
![]()
三つのインピーダンスが等しいとき、Δ回路のインピーダンスを3でわることで計算できます。上の図の場合だと、
![]()
![]()
三相交流回路におけるY-Δ変換
Y回路をΔ回路に変換するには、変換公式を用いて計算します。分子については三組の積、分母はインピーダンスから遠い端子を持つインピーダンスです。
![]()
![]()
![]()
三相交流回路におけるY-Δ変換は☝のような公式になります。また、直流回路と同様に、三相交流回路においても三つのインピーダンスが等しければ、Y回路のインピーダンスを以下のように、3倍します。
![]()
![]()
Δ-Y変換の三相電源と三相負荷の計算
三相交流回路には、三相電源と負荷の結線方法が同様のY-Y結線やΔ-Δ結線だけでなく、Y-Δ結線回路やΔ-Y結線回路があります。こうした電源と負荷で結線方法が異なる場合がありますが、一般的にはΔ-Y変換が利用されています。三相交流回路の解析にはΔ-Y変換を使用しますが、これには負荷の等価変換とで電源の等価回路があります。Y-Δ結線回路では、負荷のΔ→Y変換を利用して、Y-Y結線回路にする方法と、電源のY→Δ変換を利用してΔ-Δ結線に変換する方法があります。
三相負荷のΔ-Y変換
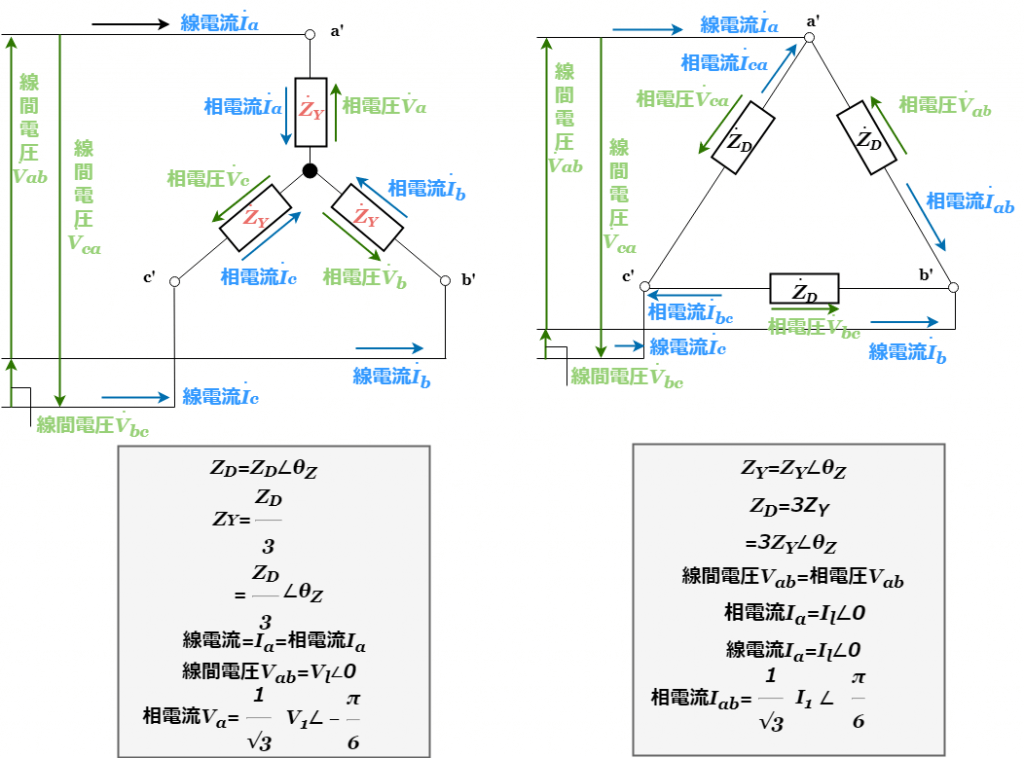
本三相交流回路は平行負荷を想定しています。ですので、簡易的な返還式になっていますが、インピーダンス角の大きさは変化しますが、インピーダンス角は変化しない点で注意が必要です。三相交流回路のΔ-Y変換を利用した回路では、Δ結線であ線間電圧と相電圧は等しくなり、相電流は大きさが線電流の![]() になり位相が
になり位相が![]() 進みます。Y結線では、線電流が相電圧と等しくなり、相電圧は大きさ線間電圧の
進みます。Y結線では、線電流が相電圧と等しくなり、相電圧は大きさ線間電圧の![]() になり、位相が
になり、位相が![]() 遅れることになります。
遅れることになります。
三相電源のY→Δ変換の計算
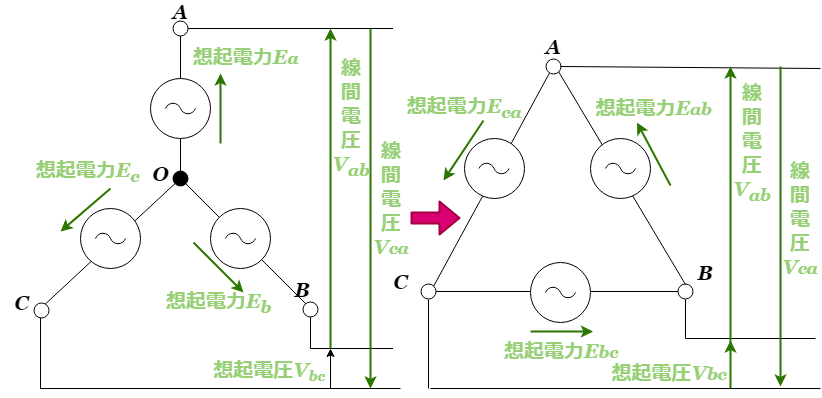
三相電源のY→Δ変換において、Y結線の線間電圧![]() は相起電力
は相起電力![]() に対して大きさが
に対して大きさが![]() 倍になり、位相差が
倍になり、位相差が![]() 進むので、
進むので、![]() を基準として、その大きさを
を基準として、その大きさを![]() とすると、以下の式(1)~(3)のようになります。
とすると、以下の式(1)~(3)のようになります。
![]()
![]()
![]()
![]()
![]()
![]()
返還後のΔ結線の相起電力の大きさを
![]()
![]()
つまり、三相電源をY→Δ変換をすることで、起電力の大きさが![]() 倍になり、位相が
倍になり、位相が![]() 進みます。三相電源のΔ→Y変換は、Y結線の相起電力と線間電圧との関係と同様になっていることがわかります。
進みます。三相電源のΔ→Y変換は、Y結線の相起電力と線間電圧との関係と同様になっていることがわかります。
三相電源のΔ→Y変換
三相電源のΔ→Y変換は、Y→Δ変換の逆になります。つまり、三相電源をΔ→Y変換すると、相起電力の大きさが![]() になり、位相が
になり、位相が![]() となることがわかります。
となることがわかります。
Δ-Y変換の例題・問題
直流回路のΔ-Y変換の例題
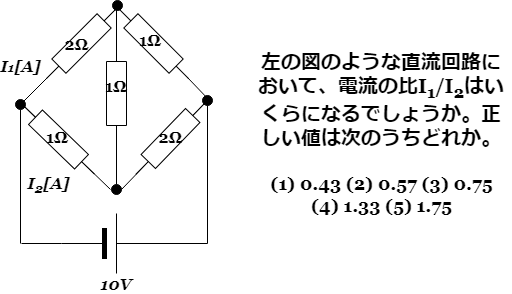
解答
①まず、この回路は2×2≠1×1ではないので、ブリッジ回路ではありません。
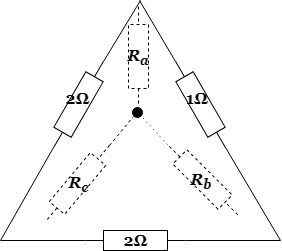
②次に、右半分のΔ結線をY結線に変換すると、以下のような回路になります。
③![]() を計算すると、以下のようになります。
を計算すると、以下のようになります。
![]()
![]()
![]()
④つまり、
![]()
![]()
![]()
よって、(3)が解答となります。
まとめ
以上のように、特に三相交流回路の解析で必要不可欠となるΔ-Y変換、Y-Δ変換の計算方法や例題を直流回路、交流回路、三相負荷、三相電源それぞれでみてきました。Δ-Y変換は最初は慣れが必要ですが、最初のうちは、変換を図化して解答していくことが重要で、そうするうちに空で変換を行うようになれます。