電験3種の合格基準
電験3種に合格するには、、、
電験3種の資格を取得するには理論、電気、機械、法規を突破しなければなりません。それぞれ6割近くの点数を取らなければ合格はできません。
ということです。。
それぞれの科目に共通して言えることは「数学」対策が必須になるということです。
数学とは一言でいってもそのレベルは相当に広いです。中学、高校レベルの数学や、大学レベルの数学といった具合に数学のレベルは幅広いものとなっています。
今回の記事では、そんな電験3種の合格に必要な数学のレベルとはどのくらいなのかということとどういう対策をしたらいいのかについてを解説します。
まずは、電験3種の学科試験において数学を抑えることの重要性を各科目ごとに見ていきましょう。
電験3種(三種)対策における数学の重要性
先ほども触れましたが、電験3種の試験科目は「理論」、「電力」、「機械」、「法規」の四科目になります。
それぞれの試験で計算問題が出題されます。計算問題を制覇することが電験3種の合格の秘訣とも言えます。
それぞれの試験科目でどのくらい計算問題が出題されているかというと、「理論」で8割、「電力」で3割、「機械」で5割、「法規」で2割程度となっています。
いかにして計算問題を解くことが電験3種合格に向けて大事かがわかるでしょう。
これらの計算問題を解くには電気の理論や知識はを押さえておくことに加えて数学の知識や計算能力が必要不可欠になります。
電験3種(電験三種)の過去問にみる数学
どんな問題が過去問では出題されているかというと以下のような問題になります。
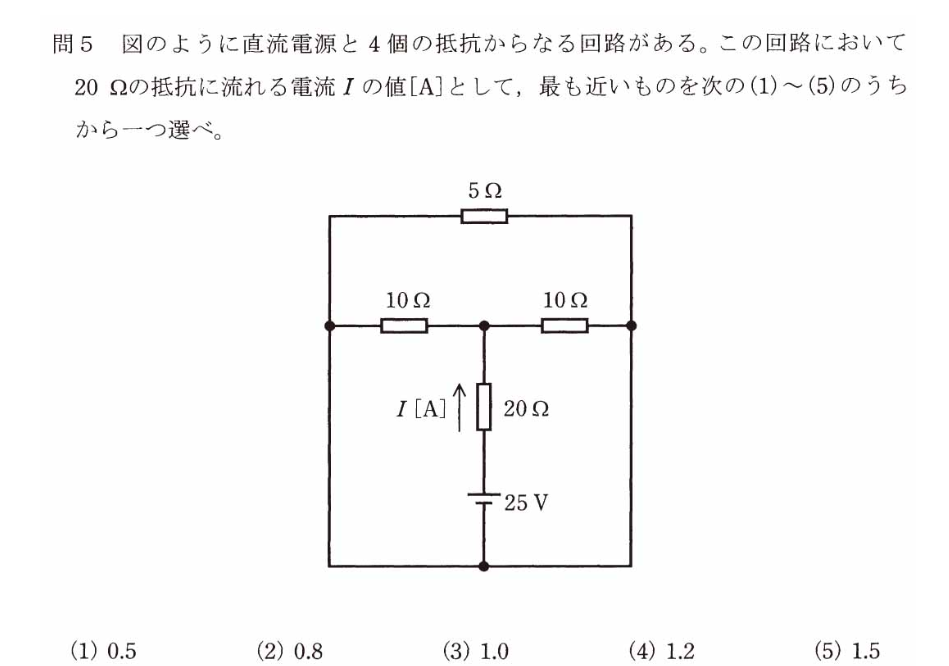
電験3種過去問：平成29年度試験理論5問
ちなみにこの問題の解答・解説は☞あります。https://www.jikkyo.co.jp/kakomon/denken3_kakomon/h29/riron/h29r_no05_kaisetsu.pdf
この問題では等価回路と合成抵抗の知識と分数の簡単な計算が必要になります。
この問題を解くには電気の知識と数学の知識が必要になります。このように電気の知識と数学の知識が必要になるような問題が多数出題されています。
電験3種(三種)合格に必要な数学のレベルその①
では実際に電験3種に合格するにはどの程度の数学レベルが必要になるのかを解説していきます。
結論から言うと、電験3種を合格するのに必要な数学のレベルというのはほとんどが「中学数学」～「高校数学」となります。ほとんどの問題が「中学数学」「高校数学」レベルの知識と計算能力＋電気の知識で解答できるような問題です。
電験3種の受験を考えている人の中には文系で、長く数学から遠ざかっている人などがいるでしょう。
中学数学とはいってもなかなか範囲が広いです。ですので、数学の中でも必要な数学の分野を紹介します。
1⃣～数と式～
数学の基本中の基本といえる数と式ですが、電験3種に特に必要なのは、「分数の計算」(電気回路の合成抵抗の計算)、「繁分数」(電気の計算で頻出)などです。
繁分数とは、例えば以下のようなものです。
![\[N=\frac{\frac{1}{\ \ 100\ \ }(\frac{1}{\ \ 100\ \ }+1)^{n} }{(\frac{1}{\ \ 100\ \ }+1)^{n}-1}\]](https://kenshoku-bank.com/column/wp-content/ql-cache/quicklatex.com-b7b86c57174ba7c7a93ada68565179c6_l3.png "Rendered by QuickLaTeX.com")
2⃣～平方根と指数～
平方根や指数の計算は、電気回路の交流の問題やインピーダンスの計算問題を解くためには必要な数学知識になります。
三平方の定理は頻出の定理ですが、これはインピーダンスや電圧・電流の大きさを求めるような計算問題で頻出で使用します。
平方根や累乗根というのは、以下のようなものです。
![\[l = \sqrt{x^2 + y^2}\]](https://kenshoku-bank.com/column/wp-content/ql-cache/quicklatex.com-d6ad45b2a370b6a4138871190b3a6b40_l3.png "Rendered by QuickLaTeX.com")
![\[\sqrt[n]{x}\]](https://kenshoku-bank.com/column/wp-content/ql-cache/quicklatex.com-147dda9d0a2a6b0e480bf58f29b7741d_l3.png "Rendered by QuickLaTeX.com")
三平方の定理というのは、直角三角形の3辺の長さの関係を表す等式のことを指します。三平方の定理を使用し、直列接続回路の計算問題などを解くことができるようになります。
3⃣～数式と方程式～
電気回路の計算で使用するキルヒホッフの法則の問題では連立方程式を説くことが要求されます。
連立方程式は、連立方程式とは2つの文字(xとy)を含み、２つの式からなる方程式のことで、以下のような形になります。
![\[\left\{ \begin{array}{lll} x + y & = & c \\ x ^2 + y^2 & = & r^2 \end{array}\]](https://kenshoku-bank.com/column/wp-content/ql-cache/quicklatex.com-170fd68a6e44c5520e2dea8e6050f3cb_l3.png "Rendered by QuickLaTeX.com")
この計算方法とキルヒホッフの第1法則、第2法則を使用すれば解答できるような問題が多数あります。
4⃣～三角比と三角関数～
三角比や三角関数というのは中学数学というよりかは高校数学で習う内容となっていますが、基礎的なものは中学数学で応用が可能です。
三角関数は電気の交流計算問題で頻出です。
三角関数とは、平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称のことを指す関数になります。公式は以下の通りです。
![\[\sin x , \cos x , \tan x \sec x , \csc x , \cot x \arcsin x , \arccos x , \arctan x\]](https://kenshoku-bank.com/column/wp-content/ql-cache/quicklatex.com-32ba4aec277eddb40b46b215e72bbef1_l3.png "Rendered by QuickLaTeX.com")
電験3種(三種)合格に必要な数学のレベルその②
ここからは少し数学のレベルがその①に比べてあがります。
5⃣～ベクトル～
ベクトルも高校数学で習う科目です。ベクトルというのは力や速度のような大きさと方向を同時に考えて数学的に計算することを言います。
電験3種の試験問題では、正弦波交流の位相や各種の電気力などを計算する際にベクトルの知識と計算方法が必須になります。
ベクトル計算では以下のような計算を行います。
![\[ \vec{a} = (a_1, \cdots , a_n) {\bf a} = \left( \begin{array}{c} a_1\\ \vdots\\ a_n \end{array} \right)\]](https://kenshoku-bank.com/column/wp-content/ql-cache/quicklatex.com-05df5ff1f1d324759fa1f0cb4a1c203f_l3.png "Rendered by QuickLaTeX.com")
6⃣～複素数～
これも高校数学で習う科目になります。
複素数というのは、実数の組〈 ａ ， ｂ 〉を、虚数単位 ｉ を使って ａ ＋ ｂｉ と解し、これを一つの数と見た場合の呼び名のことを指します。
電気工学分野では複素数により、電圧V,電流I,インピーダンスZを表現する方法のことを「記号法」といいます。この記号法による計算において複素数の知識が必要になります。
7⃣～対数、最大定理、最小定理～
対数とは、〇を何乗すれば▲になるかということを表すものになります。
対数の中でも常用対数は、増幅回路の利得計算で頻出となります。
最大定理、最小定理は、電気回路が最大電力を得るときの条件の計算の際に必要となります。
まとめ
以上、電験3種の合格に向けた数学のレベルを紹介してきましたが、電験3種の学科試験を合格するための数学は中学～高校レベルの数学の知識と計算方法がわかっていれば解けそうな問題が多いです。
数学を忘れてしまって電験3種を受けることのハードルの高さが数学にあるという声は多数あります。中学、高校の数学の教科書を引っ張り出し、今一度復習をすることで電験3種の合格可能性がたかまることでしょう。
