電気回路を学ぶ上で避けて通れないのが、「抵抗」や「電流」「電圧」といった基本概念。
その中でも「コンダクタンス」は、電気の流れやすさを示す重要な指標です。
特に、直流回路や交流回路の解析においてはもちろん、複素アドミタンス(Admittance)や電力工学の分野でも必須の概念となっています。
この記事では、そんなコンダクタンスとは何か?ということや抵抗との関係、計算・求め方についてを解説していきます。コンダクタンスを理解することは直流回路の基本を理解することや複素アドミタンスを理解するうえで重要な基本になります。

コンダクタンスとは?抵抗との関係・記号・単位
コンダクタンスとは電流の流れやすさの度合いを示す物理量
電気抵抗![]() は、簡単に言えば、電流の流れにくさの度合いを示している物理量になります。抵抗が電流の流れにくさを示すのに対し、コンダクタンスとは、電流の流れやすさの度合いを示す物理量を指します。
は、簡単に言えば、電流の流れにくさの度合いを示している物理量になります。抵抗が電流の流れにくさを示すのに対し、コンダクタンスとは、電流の流れやすさの度合いを示す物理量を指します。
コンダクタンスには記号があり、コンダクタンスの量記号は![]() 、コンダクタンスの単位には
、コンダクタンスの単位には![]() (ジーメンス)が使用されます。コンダクタンスを理解することは電気回路を勉強するうえで、重要なことですが、コンダクタンスを理解するには、オームの法則を理解しておく必要があります。
(ジーメンス)が使用されます。コンダクタンスを理解することは電気回路を勉強するうえで、重要なことですが、コンダクタンスを理解するには、オームの法則を理解しておく必要があります。
コンダクタンスは「コンダクタンス![]() は抵抗
は抵抗![]() の逆数」と定義されます。ですので、コンダクタンスと抵抗の間には以下のような関係が成立します。
の逆数」と定義されます。ですので、コンダクタンスと抵抗の間には以下のような関係が成立します。
![]()
コンダクタンスと抵抗の関係は☝のような関係式で示すことができますが、もちろん、コンダクタンス![]() の逆数が抵抗
の逆数が抵抗![]() ということもできます。たとえば、
ということもできます。たとえば、![]() の抵抗は
の抵抗は![]() のコンダクタンスと表現することができるようになるのです。
のコンダクタンスと表現することができるようになるのです。
コンダクタンスは、抵抗回路をコンダクタンスで表現することが可能です。それは、オームの法則における電圧、電流、抵抗の関係を、電圧、電流、コンダクタンスの関係に置き換えてみると、以下のようになります。
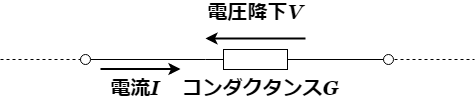
![]()
![]()
![]()
オームの法則を数学的な表現で表すならば、「導体の2点間の電圧![]() は、2点間を流れる電流
は、2点間を流れる電流![]() に比例する。その比例定数が2点間の抵抗
に比例する。その比例定数が2点間の抵抗![]() である。」ということができます。ここでいう比例定数とは、比例関係を示す数式における一定の数値のことで、比例係数ともいうことができます。このことを数式で表現すると、
である。」ということができます。ここでいう比例定数とは、比例関係を示す数式における一定の数値のことで、比例係数ともいうことができます。このことを数式で表現すると、![]() となります。
となります。
同じ王に、「導体の2点間を流れる電流![]() [A]は、2点間の電圧
[A]は、2点間の電圧![]() に比例します。その比例定数が2点間のコンダクタンス
に比例します。その比例定数が2点間のコンダクタンス![]() である」ということもできます。これを数式にすると、
である」ということもできます。これを数式にすると、![]() となります。この式も同様にオームの法則を示しているのです。
となります。この式も同様にオームの法則を示しているのです。
コンダクタンスの計算・合成コンダクタンスとは?
複数の抵抗を一つにみなしたものを合成抵抗といいます。抵抗において合成抵抗が可能なように、コンダクタンスにおいても複数のコンダクタンスを一つのコンダクタンスにみなしたものを合成コンダクタンスといいます。合成コンダクタンスの計算は、直列接続の計算式と並列接続の計算式が、合成抵抗と合成コンダクタンスで逆になります。
並列接続の合成コンダクタンスの計算
コンダクタンスにおいて、並列接続の方が計算はシンプルで簡単ですが、並列接続の合成コンダクタンスは計算が面倒です。まずは、並列接続の合成コンダクタンスから解説しますが、並列接続の合成コンダクタンスは加算でいいのです。並列接続の合成コンダクタンスの公式は、以下のようになります。
並列接続された![]() のn個のコンダクタンスの合成コンダクタンスを
のn個のコンダクタンスの合成コンダクタンスを![]() とすると、
とすると、
![]()
直列接続の合成コンダクタンスの計算
コンダクタンスを直列接続した場合、それぞれのコンダクタンスの逆数の和が合成コンダクタンスの逆数になります。直列接続の合成コンダクタンスの公式は次のようになります。直列接続された![]() のn個のコンダクタンスの合成コンダクタンスを
のn個のコンダクタンスの合成コンダクタンスを![]() とすると、
とすると、
![]()
となります。この式は並列接続の合成抵抗の公式と、式の構造は同じです。並列接続された抵抗器の情報が抵抗であったとしても最初にコンダクタンスに置き換えれば加算で計算することが可能です。結果として、合成抵抗を求められている場合、抵抗のまま計算してもコンダクタンスに置換して計算しても計算過程は同じです。しかし、量記号による数式を展開していく場合、コンダクタンスに置き換えた方が数式はシンプルになります。
抵抗およびコンダクタンスの直列・並列接続
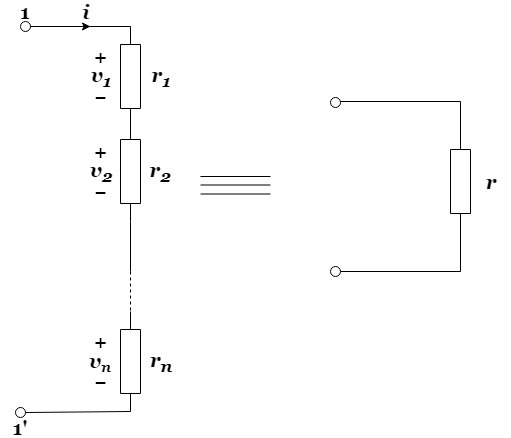
上にみたコンダクタンスを求める公式を抵抗を用いて証明していきます。まず、抵抗の直列接続についてを考察します。図1に示すように、n個の抵抗を直列に接続し、電流![]() を流すと、1-1’間の電圧降下
を流すと、1-1’間の電圧降下![]() は、次の式になります。
は、次の式になります。
![]()
全体の抵抗を![]() とすると、
とすると、
![]()
と表すことができます。次に図2のように、n個の抵抗を並列接続し、1-1’間に電圧![]() を加えると、各抵抗に流れる電流は、
を加えると、各抵抗に流れる電流は、
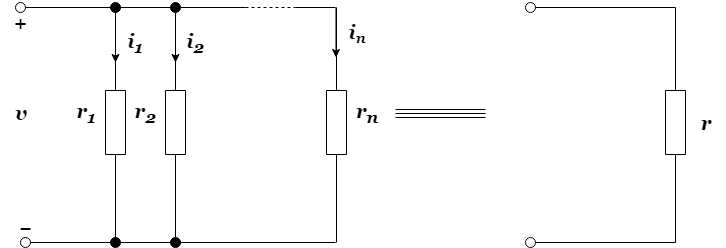
![]()
となります。ここで全体の電流![]() は、以下のようになります。
は、以下のようになります。
![]()
1-1’間の抵抗を![]() とすると、以下のようになります。
とすると、以下のようになります。
![]()
コンダクタンスの直列・並列接続の場合にも同じようにして、直列接続では、
![]()
並列接続においては、
![]()
となります。抵抗を用いてコンダクタンスの計算を理解するとよいでしょう。
よくある質問
コンダクタンスはどんな場面で使われるの?
電力系統の安定性解析や電流解析ツールでの簡略化、アドミタンスマトリクスの構築のような技術分野で使用されます。
コンダクタンスの単位「ジーメンス」とは?
コンダクタンスの単位は S(ジーメンス) で、かつては「モー(mho)」という逆スペル表記も使われていました。
この単位は、以下の関係に由来しています。
つまり、1オームの抵抗の逆数が1ジーメンスということになります。
ジーメンスは国際単位系(SI)にも正式に採用されており、インピーダンスの逆数や回路設計の標準単位として使われています。
まとめ
以上のように、電気回路を理解するうえで、重要となるコンダクタンスについてを解説してきました。コンダクタンスの単位はジーメンスであり、抵抗の逆数![]() となることを抑えておきましょう。コンダクタンスの計算・合成コンダクタンスについては直列接続と並列接続で、公式が抵抗の合成抵抗と逆になることを覚えておく必要があります。
となることを抑えておきましょう。コンダクタンスの計算・合成コンダクタンスについては直列接続と並列接続で、公式が抵抗の合成抵抗と逆になることを覚えておく必要があります。