テブナンの定理とは？証明や例題・問題を踏まえて解説

電気回路の解析の手法の一つであり、第3種電気主任技術者(電験3種)の理論の問題でも重要なテブナンの定理とは一体どのような理論なのか？ということを証明や問題を通して紹介します。

テブナンの定理とは？

テブナンの定理：テブナンの等価回路と公式

テブナンの定理とは、「電源を含む回路の任意の端子a-b間の抵抗Rを流れる電流Iは、抵抗Rを除いてa-b間を解法したときに生じる解法電圧と等しい起電力と、回路内のすべての電源を取り除いてa-b間から回路を見たときの抵抗Rによってと表すことができます。」

簡単にいうと、テブナンの定理とは、直流電源を含む回路において特定の岐路の電源を求めるときに、特定の岐路を除く回路を単一の内部抵抗のある電圧源に変換して求める方法です。この電圧源のことをテブナンの等価回路といいます。等価回路とは、電気的な特性を変更せず、ある電気回路を別の電気回路で置き換えることができるような場合に、一方を他方の等価回路といいます。

回路内の一つの抵抗を流れる電流のみを求める際に便利になるのがテブナンの定理です。テブナンの定理は東京大学の教授鳳(ほう)教授と合わせ、鳳-テブナンの定理とも称されますし、テブナンの等価回路を投下電圧源表示ともいいます。

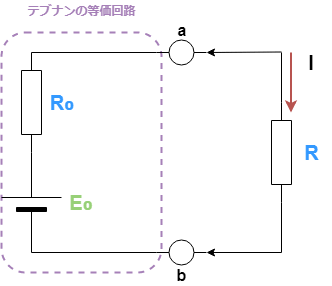
図1起電力と内部抵抗

図1のように、起電力と抵抗を含む回路網において任意の抵抗Rに流れる電流Iは、以下のようなテブナンの定理の公式により求めることができます。

ここで、は、抵抗Rがないときに、端子a-b間で生じる電圧のことです。また、は、回路網の起電力を除き、その箇所を短絡して端子間a-b間から回路網内部をみたときの合成抵抗となります。電源を取り除く際に、電圧源の場合は短絡、電流源の場合は開放にします。開放された端子間の電圧のことを開放電圧といいます。

テブナンの定理の証明

電気工学における理論の証明は得てして簡潔なものが多いですが、テブナンの定理の証明は「テブナンの定理は重ね合わせの定理を用いて説明することができる」という文言がなされることが多いです。

テブナンの定理の証明方法についてはいくつかあり、他のHPや大学の講義、高校物理の教科書等で証明されています。

重ね合わせの定理によるテブナンの定理の証明は、以下のようになります。

1. 端子a-b間に任意の抵抗と開放電圧の電圧源を接続します。Nは回路網を指します。
   
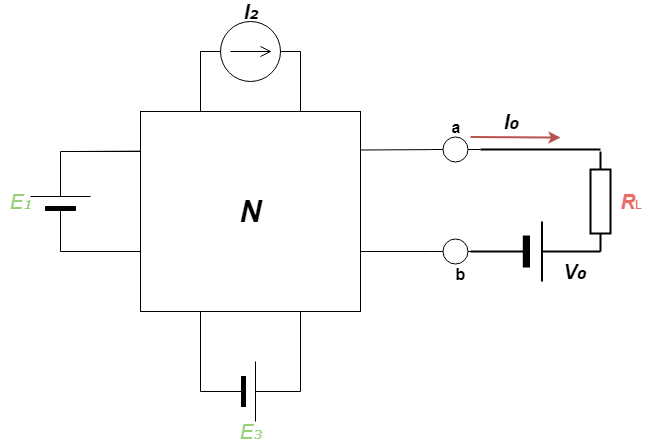
2. ここで、端子間a-bを流れる電流I₀はゼロとします。開放電圧がV₀で、端子a-bから見た抵抗はR₀となります。
3. 電流I₀は重ね合わせの定理を用いてI’とI”の和になりますので、となります。
   
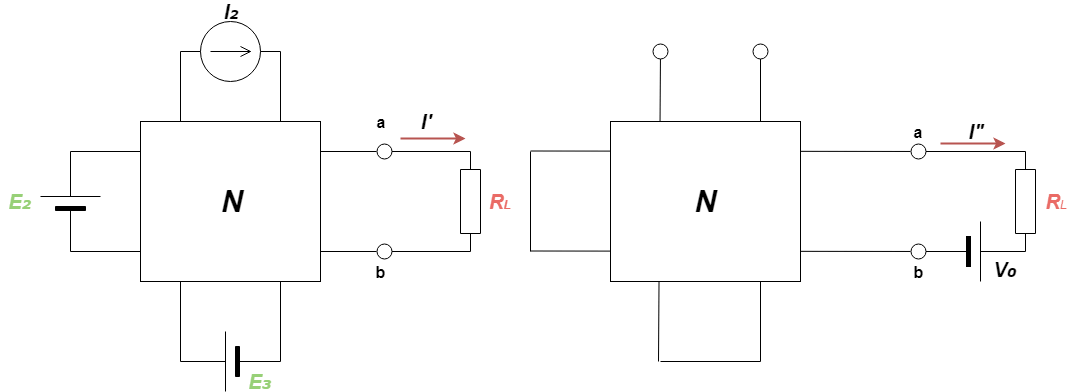
4. このとき、となり、と導くことができます。
5. より、
   ・・・・・i
6. この(i)式が任意のに対して成り立つといえるので、この回路は起電力、内部抵抗の電圧源と等価になります。(等価回路)

テブナンの定理を証明するうえで、重ね合わせの定理を用いることで簡易的に証明することができます。このほかにもいくつか証明方法があるかと思われるので、HPや書籍などで確認できます。

テブナンの定理の例題・問題

テブナンの定理の例題・問題

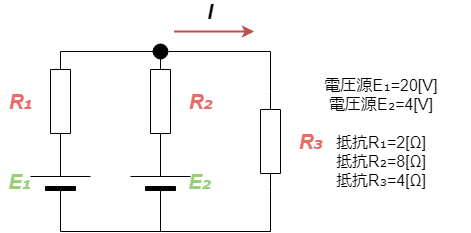
図2テブナンの定理の例題

1. 解析対象となる抵抗を取り外し、端子間を開放する
   抵抗R₃に流れる電流Iを求めるにはいくつかの手順を踏みます。図2の回路の抵抗R₃を取り外し、以下の図のように端子間a-bを作ります。
   
   

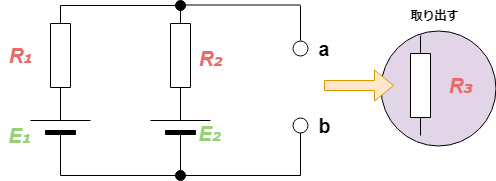
   図3抵抗を取り出す

    

2. 端子間の開放電圧を求める
   次の手段として、抵抗R₃がないときの作成した端子a-b間の解法電圧V₀を求めます。回路構造によっては解法は異なりますが、キルヒホッフの法則を用いると計算がはかどります。
   この左側の回路で、循環電流I’を求めると、
   
   となります。このとき、20Vから2Ωを引くと、
   
   となり、テブナンの等価回路の電圧V₀は16.4Vになります。
3. 電源を取り外し、端子間の抵抗を求めます。
   回路網の内部抵抗R₀を求めるには、取り外した部分は短絡するので、2Ωと8Ωの並列合成抵抗R₀を和分の積で求めることができます。
   [Ω]
   
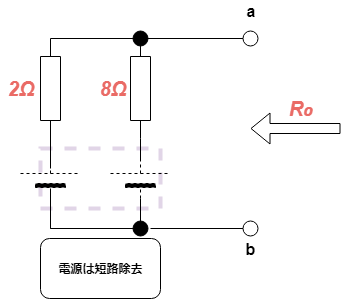
4. テブナンの定理に則って電流を求めると、
   
   
   となります。

まとめ

以上のようにテブナンの定理の公式や証明、例題・問題についてを紹介してきました。テブナンの定理を使用すると、暗算で計算できる問題があったりするので、その公式と使用するタイミングについてを抑えておく必要があるでしょう。