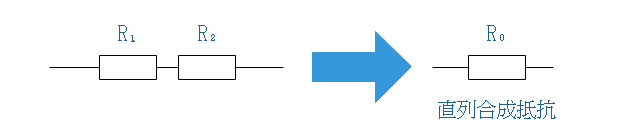電気に関する基礎的な知識として合成抵抗があります。合成抵抗の問題は電験の資格試験や電気工事士試験などで頻出の知識となります。今回はそんな合成抵抗とは何か、その計算方法や問題、さらには分圧・分流についてを紹介します。
合成抵抗とは
2個以上の抵抗を直列や並列に接続した場合の全体の抵抗のことを「合成抵抗」といいます。電気回路において複数の抵抗を一つの抵抗に置き換えたときの抵抗を意味しますが、合成抵抗には、直列接続の場合と並列接続の場合、抵抗の個数などでその計算式が変わってきます。それぞれの計算方法を自由に使いこなせることが理想的です。
2個以上の抵抗を1列に接続する方法のことを「直列接続」といいます。一方、抵抗の両端を同じところに接続する方法を抵抗の「並列接続」といいます。
合成抵抗の計算方法
合成抵抗の計算方法は、抵抗の個数で計算式が変わってきます。合成抵抗の電気回路において、抵抗の個数が2個の場合と、抵抗の個数がn個の場合でそれぞれみていきましょう。
抵抗が二個の場合の計算
直列接続の場合
2個の抵抗を直列接続した場合の直列合成抵抗
は。2個の抵抗値の和になります。
つまり、
[Ω]となります。
直列合成抵抗
例えば、R₁=30、R₂=60のとき、R₀=90[Ω]となります。2個の抵抗の場合、直列に並んだ抵抗を足し合わせていくことでR₀が求まるので、直列合成抵抗の計算はシンプルなものになります。
並列接続の場合
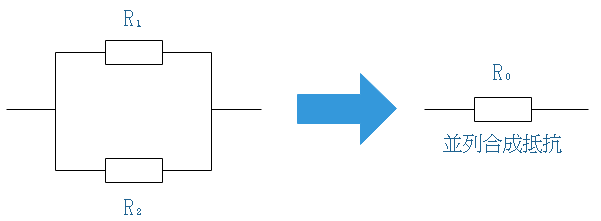
2個の抵抗を並列に接続したときの並列合成抵抗は、2個の抵抗値の和分の積となります。和分の積というのは、分子が掛け算で、分母は足し算のことをいい、和分の積で並列合成抵抗は計算できます。
つまり、
となります。
並列合成抵抗
例えばR₁=20、R₂=60のとき、
[Ω]となります。
この並列合成抵抗の計算は、簡易計算することが可能です。公式の分母と分子をR₁で割って計算すると、以下のようになります。
[Ω]
このようにして2つの抵抗値の非R₂/R₁が容易に求まるときに関しては計算速度を速めるという点で効率的です。計算例でだしたR₁とR₂の抵抗値の比が60/20=3でした。このような抵抗値の比が整数倍の時は便利となっています。ただし、この並列合成抵抗の場合は2個の抵抗を想定していますので、、3個以上の抵抗だとこの公式は当てはまりません。問題文を見て抵抗の個数に注意をしておく必要があります。
抵抗がn個の場合の計算
抵抗がn個の場合の合成抵抗の計算は少し複雑になります。2個の抵抗の場合と同様に直列合成抵抗の場合、並列合成抵抗の場合をみていきましょう。
n個の直列合成抵抗の場合
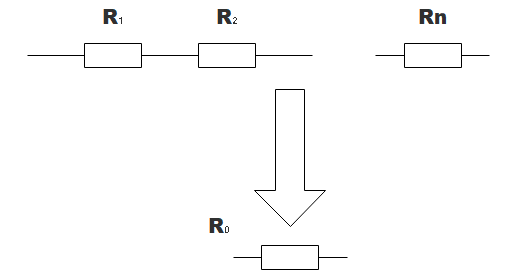
n個の直列合成抵抗は、各抵抗の和を求めることで計算できます。
つまり、
[Ω]
n個直列合成抵抗
となります。抵抗が、n個の場合でも2個の場合と同様の足し合わしていく計算で求めることができます。
n個の並列合成抵抗の場合
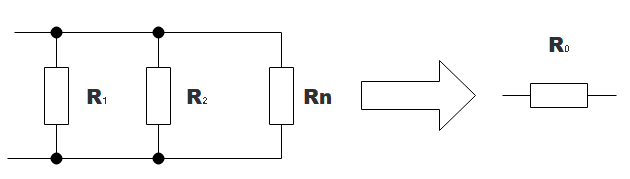
n個の並列合成抵抗は、各抵抗の逆数の和を求め、さらに逆数を求めることで計算できます。その計算式は以下のようになります。
[Ω]
n個並列合成回路
合成回路計算の例題・問題
例題：短路された合成抵抗に関する電験3種の問題
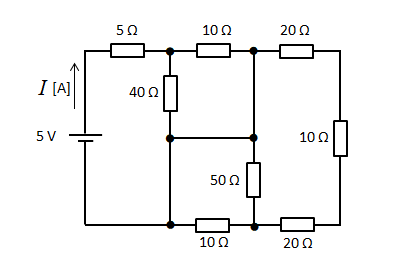
図に示すような抵抗の直並列回路がある。この回路に直流電圧5[V]を加えたとき、電源から流れる電流I[A]の値として近いものは何か
電験3種合成回路過去問(H25.理論.問8)
(1)0.2 (2)0.4 (3)0.6 (4)0.8 (5)1.0
解答・解説
合成抵抗電験3種解答
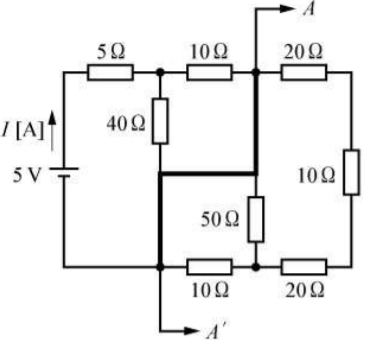
この問題の解答方法はいくつかありますが、上図のように題の電気回路を整理します。この図で示した太線の部分は短路されています。ですので、A-A’の右側部分は除去して考えることができます。
すると、まず、和分の積によって以下のように計算することができます。
と計算できます。ですので、解答は(2)の0.4になります。
短路が含まれた場合の合成回路の計算は電流の性質に着目する必要があります。電流の性質には「より小さいほうの抵抗を流れる」という性質があります。問題の図では電流が流れ、5Ωの抵抗を通過し、10Ωの抵抗と40Ωの抵抗に分岐します。その後の電流は短路(抵抗0Ω)へながれます。このような複数の抵抗が問題で与えられているさいには、電流の流れを意識することが重要でしょう。
