電気回路におけるキルヒホッフの法則とは？公式や例題について

電験3種の理論の科目のみならず、電気回路を理解するうえで重要となる法則「キルヒホッフの法則」とは一体どんな法則なのか？ということを例題を交えて解説します。

1 キルヒホッフの法則とは？
2 キルヒホッフの法則の第1法則と第2法則(公式)
3 キルヒホッフの法則の例題・問題
4 まとめ

キルヒホッフの法則とは？

電気回路解析の代表的な手法がキルヒホッフの法則

キルヒホッフの法則は、複雑な直列回路の解析の際に用いる法則の一つです。しばしば、電気回路の学習においてオームの法則の次に抑えるべき理論であるとされます。複雑な電気回路の解析においては、電圧、抵抗、電流についての関係式を作り、その方程式を解くことで回路の解析を行います。キルヒホッフの法則はそのうちの一つで代表的な電気回路解析方法です。

キルヒホッフの法則とは、「電気回路において任意の節点に流れ込む電流の総和、任意の閉路の電圧の総和に関する法則」です。キルヒホッフの法則は、ドイツの物理学者であるグスタフ・キルヒホフが1845年にが発見し、その名にちなんでキルヒホッフの法則と名付けられました。

キルヒホッフの法則には、2つの法則があり、電流に関するキルヒホッフの第1法則と、電圧に関するキルヒホッフの第2法則があります。キルヒホッフの法則において解析の視点となるのは、電気回路の節点、枝、閉回で回路の状態を把握することです。

節点、枝、閉回路とは？

節点

節点とは、電流の分岐や合流が発生する可能性がある点で、基準からの電圧が独立したもので、よくa,bといった表現で節点を表します。

枝

枝とは、節点と節点に連結される分岐のない経路のことをいい、枝路ともされます。電流の分岐や合流がないので、枝は全体を同じ大きさの電流が流れることになります。

閉回路

閉回路とは、回路中のある点から出発し、いくつかの節点と枝を経由し、出発点に戻った際に、そのたどった経路のことで、ループという呼ばれ方もします。

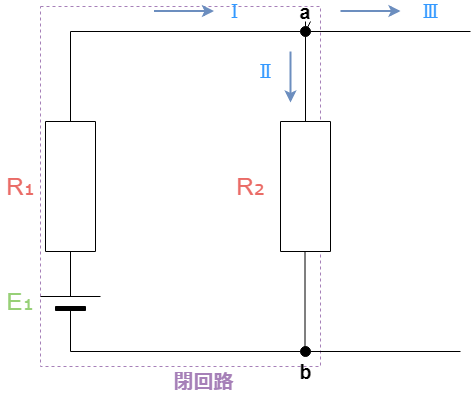
図1節点と枝と閉回路についての回路

キルヒホッフの法則における電気回路の解析の視点について押さえたところで、キルヒホッフの法則には第1法則と第2法則の二つの法則があると先ほど記述しました。次にそれぞれについてを見ていきます。

キルヒホッフの法則の第1法則と第2法則(公式)

キルヒホッフの第1法則(電流側)とその公式

キルヒホッフの第1法則は、電流に関する法則でした。そうしたこともあり、キルヒホッフの電流則とも言われます。キルヒホッフの第1法則は「回路中の任意の節点に流入する電流の総和は0である」と説明されます。簡単に言うと、「接続点に入る電流と出る電流は同じで、その総和は等しい」のです。つまり、キルヒホッフの第1法則は加算により導くことができます。

次の図2にあるように、接続点aに流入する電流 $I_0$ と、流出する電流( $I_1+I_2$ )は等しくなるのです。この関係をキルヒホッフの第1法則といいます。キルヒホッフの第1法則の公式は以下のようになります。

$I_0=I_1+I_2$ [A]

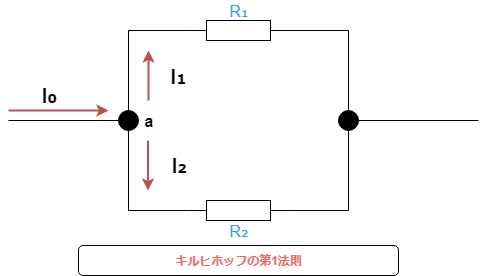
図2キルヒホッフの第1法則

このような式をキルヒホッフの電流則に基づく電流方程式、節点方程式と呼びます。電流則は回路中のすべての点に当てはまる法則で、回路中の任意の点に流入する電流の総和はゼロであるというような説明をすることもできます。

キルヒホッフの第1法則の公式は電気回路の解析における基本となっております。公式を抑えておきましょう。

キルヒホッフの第2法則(電圧側)とその公式

キルヒホッフの第2法則は、電圧に関する法則なのでキルヒホッフの電圧則と呼ばれることもあります。キルヒホッフの第2法則は「回路中の任意の閉回路を一定の方向にたどった際に、その電圧の総和はゼロになる」と説明されます。抵抗に電流が流れるとオームの法則による電圧が抵抗に生じます。このことを抵抗の電圧降下と呼び、電気回路をたどるときに、電圧を上昇させる起電力があったり、電圧降下があったりしますが、電気回路を一周すると、電圧の総和はゼロになるのです。

これを言い換えると、「閉回路における電源の電圧の和は、抵抗の電圧降下の和になる(起電力の総和=電圧降下の総和)」ということができます。

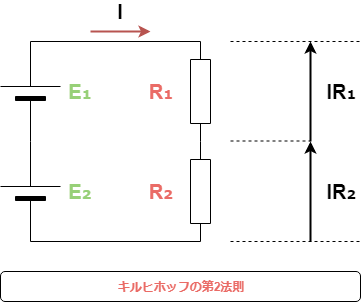
図3のような閉回路内の起電力(電源の電圧)の和( $E_1+E_2$ )は、閉回路内の電圧降下の和( $IR_1+IR_2$ )に等しくなります。このような関係のことをキルヒホッフの第2法則と呼びます。キルヒホッフの第2法則の公式は以下のようになります。

$E_1+E_2=IR_1+IR_2$

図3キルヒホッフの第2法則

このような公式を電圧方程式や閉路方程式と呼ぶことがあります。電圧方程式を使用する際には、「起電力については、たどっていく方向に電圧が上がる場合はプラスの電圧、たどっていく方向に電圧が下がる場合はマイナスの電圧になる。電圧降下については、たどっていく方向と電流が同じ場合はプラスの電圧降下、たどっていく方向と電流が逆の場合はマイナスになる。」ということに留意する必要があります。

キルヒホッフの法則の例題・問題

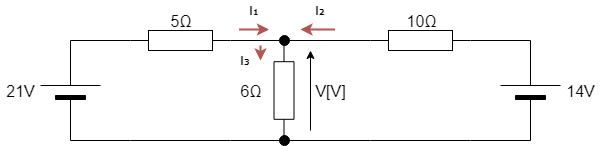
図4キルヒホッフの法則の例題

問題
上の図4の電流をI₁、I₂、I₃と仮定し、図4のような直列回路において、抵抗6Ωの端子電圧の大きさVの値を求めよ。

解法

I₁とI₂節点aと置き、点aにキルヒホフの第1法則の公式を適用すると、
$I_1+I_2=I_3$ ・・・・・(1)
キルヒホッフの第2法則より、
閉回路(左): $21=5I_1+6I_3$ ・・・・・(2)
閉回路(右): $14=10I_2+6I_3$ ・・・・・(3)
式(1)から $I_1=I_3-I_2$ となり、これを式(2)に代入して整理すると、
$21=5(I_3-I_2)+6I_3$
$21=-5I_2+11I_3$ ・・・・・(4)
式(3)/2より、 $7=5I_2+3I_3$ ・・・・・(5)
式(4)＋(5)より
$28=14I_3$
$I_3=28/14=2A$
抵抗6Ωの端子電圧Vは、
$V=2\times6=12V$