施工管理の国家資格のうちの一つである「管工事施工管理技士」の資格は受験資格の実務経験要件のハードルが高く、試験の難易度も高い試験です。そんな管工事施工管理技士の資格を目指す理由はそれぞれありますが、気になることのうちの一つとして「管工事施工管理技士の年収は高いのだろうか?低いのだろうか?安定しているのだろうか?」などといった年収・給料にまつわる悩みはあるでしょう。
そこで、転職求人サイト「建職バンク」の管工事施工管理技士を対象にした求人情報から管工事施工管理技士の年収を調査しました。また、求人情報から管工事施工管理技士のモデル年収についても紹介します。
▼転職をお考えの方はこちらもどうぞ
1級管工事施工管理技士の求人を検索
2級管工事施工管理技士の求人を検索
電気業界最大級の転職・求人情報サイトで、ピッタリの求人を見つけましょう。

管工事施工管理技士[1級・2級]の年収の分布とは?平均年収は?
管工事施工管理技士は1級の方が2級より高年収求人が多い
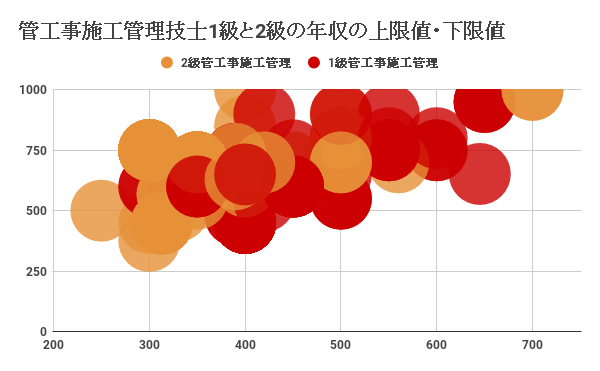
管工事施工管理技士の年収の分布1級と2級で、求人情報からその上限値と下限値で分布を見てみましょう。
上の図は管工事施工管理技士の年収の分布を1級と2級でそれぞれ調査した分布図になります。この分布図を見ると明らかに1級管工事施工管理技士に対する求人情報の年収が高年収帯に位置していることがわかります。
1級管工事施工管理技士の年収の下限値は400万円~600万円帯に多く分布しており、上限値年収は500万円~750万円帯に多く分布していることがわかります。
一方、2級管工事施工管理技士の年収は下限値で300万円~400万円に多く分布しており、上限値年収は400万円~600万円帯に多く分布していることがわかります。
管工事施工管理技士の年収別の求人数
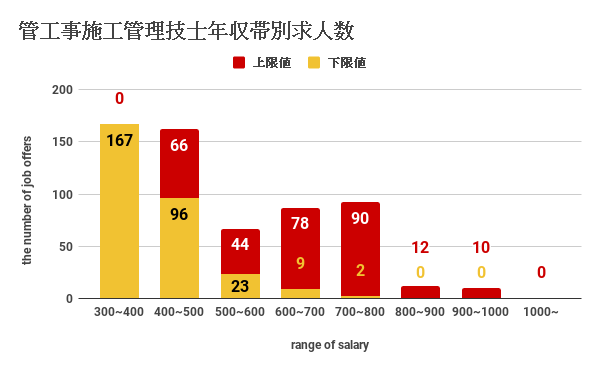
次に管工事施工管理技士を対象にした年収幅別の求人数を年収上限値と下限値で見ていきましょう。
管工事施工管理技士の求人をベースにした年収では、下限値年収では3年収300~400帯に求人数が167件、年収400~500万円帯に求人数が96件となっています。管工事施工管理技士の年収の下限値では、300万円から500万円の間の求人情報が多いことがわかります。
そして、管工事施工管理技士の年収の上限値の求人数では、600万円~700万円に78件、700万円~800万円に求人数が90件と多く分布していることがわかります。管工事施工管理技士の年収の上限値は600~800万円帯に多く求人があるようです。
求人をベースにした管工事施工管理技士の年収のボリュームゾーンを算出すると、おおよそ年収400万円から600,700万円となっているようです。もちろん目安に過ぎないので、かならずしも管工事施工管理技士の年収がこの年収帯に位置しているとは限りません。
そして、管工事施工管理技士の年収の下限値の平均は、387万円となり、年収の上限値は630万円となりました。求人情報をベースにした管工事施工管理技士の平均年収は、、509万円となっているようです。日本人の平均年収が420万円とされているので、管工事施工管理技士の年収は平均よりも高い給料となっていることがわかります。
続いて、管工事施工管理技士の年収を1級と2級に分けて細かく見ていきましょう。1級と2級で年収が違うことは先ほどの分布図からわかりましたが、実際にどのくらいの金額となっているのでしょうか。
管工事施工管理技士の年収を1級と2級別に調査!
1級管工事施工管理技士の平均年収は507万円⁉
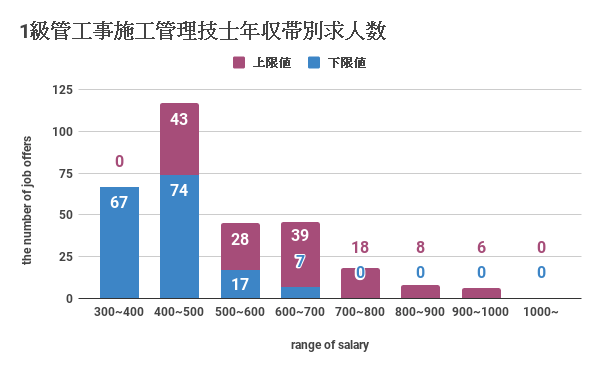
1級管工事施工管理技士の年収帯別求人数は☝のグラフのようになりました。年収の下限値では300~500万円帯に多くの求人があるようです。1級管工事施工管理技士の年収上限値では、400~700万円の求人が多く位置しているようです。1級管工事施工管理技士の求人の中には年収1000万円の求人もあるので、1級管工事施工管理技士の年収は高いといえるでしょう。年収1000万円を提示する求人は日本に多くはありませんが、1級管工事施工管理技士の資格保有者の中には年収1000万円を稼ぐ人もいるようです。
1級管工事施工管理技士の年収の下限値の平均は、427万円となり、年収の上限値の平均は589万円となりました。また、1級管工事施工管理技士の平均年収は507万円となることがわかりました。1級管工事施工管理技士の年収は求人情報をベースにすると、高い年収水準であることがわかります。
2級管工事施工管理技士の平均年収は498万円⁉
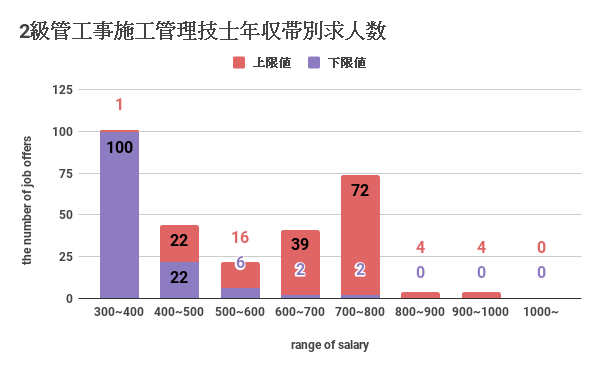
2級管工事施工管理技士の年収帯別の求人数は上のグラフのようになりました。2級管工事施工管理技士の年収帯別の求人数をみると、年収下限値で300~400万円の求人が多くあり、年収の上限値で見ると、700~800万円帯に多く分布していることがわかります。2級管工事施工管理技士の年収でなかなか1000万円を提示する求人はないのですが、1級同様に数件だけは年収1000万円を提示するものがあります。
2級管工事施工管理技士の年収の下限値の年収の平均は351万円、年収の上限値の平均は、646万円となりました。1級が589万円なのに対し、2級の方が年収上限値の平均では646万円となっていました。2級では下限値こそ低いものの、上限値年収では1級より高くなっていますが、2級の場合、2級管工事施工管理技士の資格以外の資格(例えば土木施工管理、建築施工管理、電気主任技術など)を複数保有していることが求められているようです。それゆえに年収の上限が高くなっているようです。2級管工事施工管理技士の平均年収は498万円となっていることがわかりました。*あくまで求人情報を基にした独自調査の数値となります。
管工事施工管理技士のモデル年収ってどれくらい?
次に実際の管工事施工管理技士を対象にした転職サイト「建職バンク」内にある求人情報から管工事施工管理技士のモデル年収を調査していきます。モデル年収で、貰える年収の想定がしやすくなります。
管工事施工管理技士のモデル年収その①現場代理人の求人

管工事施工管理技士のモデル年収(【管工事施工管理技士2級以上】空調設備工事の現場管理[神奈川県横浜市]求人はこちら)
管工事施工管理技士の資格を必須としている求人です。こちらの求人は空調設備工事の現場代理人枠での募集となっています。管工事施工管理技士ならば、1級でも2級でも応募可能な求人で、サブコンでの勤務になります。年収に関しては450~600万円となっており、管工事施工管理技士の年収のボリュームゾーンとなっていることがわかります。
管工事施工管理技士問わず、施工管理の仕事はきついことが多く、病気で倒れたりすることもある仕事です。ですが、きつさに見合った待遇を指定くれる会社も多くあります。管工事施工管理技士の資格を活かした求人は多くありますし、きつすぎない求人もあります。管工事施工管理技士に対するサブコンを中心とした需要は高いですし、くいっぱぐれない資格職といえます。
管工事施工管理技士のモデル年収その②年収1000万円の求人

管工事施工管理技士のモデル年収その②(【海外】機械設備設計・積算職※住友グループ数少ない電気インフラを支える総合エンジニアリング企業:求人はこちら)*写真はイメージ
こちらの求人は年収上限1000万円を提示する管工事施工管理技士の資格保有者を対象にした求人です。子の求人では、東南アジア等海外転勤もある求人で、ゼネコン・サブコンでの経験が求められる即戦力を募集する求人となっています。空調プラントの施工管理を担える仕事でインフラを支える仕事であるので、非常にやりがいにあふれた求人となっています。管工事施工管理技士の資格を保有していると、海外で活躍できる可能性もあるので、非常に需要のたかい資格職であるといえます。
管工事施工管理技士の資格を活かして年収を上げるには?[転職]
今の会社よりいい待遇で活躍したいと思ったときに転職は一つの手段です。もちろん、転職することはキャリアに傷をつけることにもなりえますし、必ずしも良いものではありません。ですが、現状の年収に満足していない、会社が業績不振である、今より休日が多い会社へ移籍したい、やりがいの感じられる仕事に就きたい、資格を活かした仕事がしたいなどなどの要因は転職の理由になります。そうした際に資格を活かして年収をいかに上げるかということについては、転職エージェントに相談するなどの手段があります。
現在の空調設備工事などの設備工事業は堅調に完成工事高を伸ばしていっています。そんな市場環境の中、管工事施工管理技士の資格を活かした転職は企業側の採用ニーズが高いのです。1級と2級、監理技術者か主任技術者かの境はなく、管工事施工管理技士の資格を保有し、経験を積んでいる人材には高い年収が提示されることがあるのです。また、管工事施工管理技士の資格だけでなく、電気工事施工管理技士の資格も保有し、管の知識と電気の知識を併せ持ち、なおかつ経験も有する人材への期待値は高いようです。
ですので、もし仮に管工事施工管理技士として現状の年収に満足していない場合、電気の知識と経験を身に着けたうえで転職をする場合、年収もそれに応じた金額になる可能性があります。その背景には空調設備に付随する受変電設備の知識と点検のスキルを持っている人材はなかなかいないとされているからです。言い換えると、動力設備全体の施工と保守ができる人材です。もし管工事施工管理技士の資格を活かした転職を考えている際は「建職バンク」に相談してみてはいかがでしょうか。
まとめ
以上のように、管工事施工管理技士の年収を1級と2級に分けて紹介し、モデル年収からその年収についてを紹介してきました。管工事施工管理技士の年収は1級、2級問わずに日本人平均年収よりも高い年収を提示する求人が多くあります。資格保有者も電気や土木、建築と比較すれば多くはありません。管工事施工管理技士に対する需要は高いといえるでしょう。

キャリアアドバイザーには元施工管理技士など、建設業界の現場と人材市場に精通した専門スタッフが在籍。累計登録者数19万人超(※2025年12月時点)の支援実績と、日々のアドバイザー活動から得られる「現場のリアルな一次情報」をもとに、求職者の皆様に役立つ正確な情報を発信しています。